I. 서 론
II. AMC 송수신모델 및 임계값 검출 알고리즘
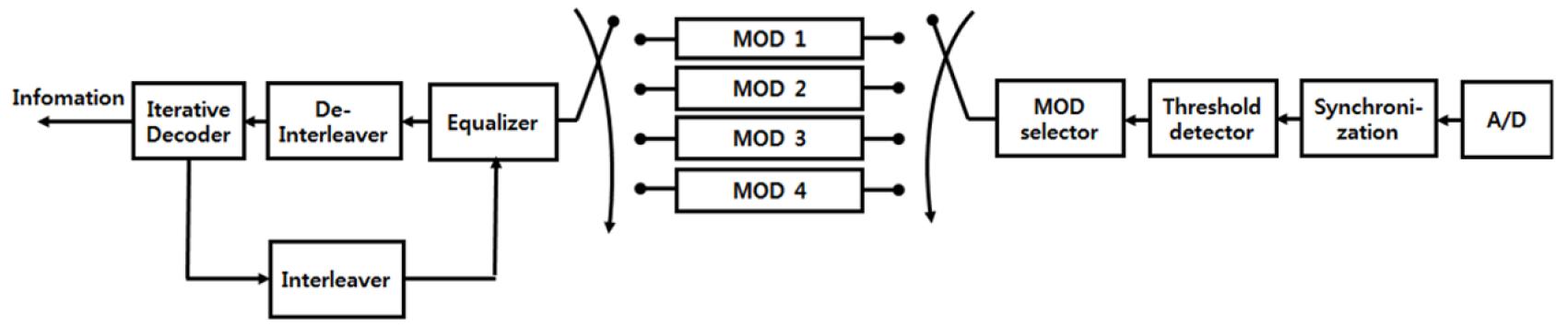
2.1 AMC 송신부 모델
2.2 AMC 수신부 모델
2.3 임계값 결정 파라메타 검출 기법
III. 실험결과
IV. 결 론
I. 서 론
수중에서는 직접파와 더불어 해수면과 해저면의 반사 등으로 인해 다중경로 전달을 포함한 다양한 특성으로 수중음향통신의 성능 저하를 일으키며 음파가 전달되는 형태가 복잡하다. 수중음향통신의 성능을 결정하는 요인에는 음향 신호의 거리에 따른 전달 손실과 다중경로 전달 과정으로 인한 간섭 신호, 배경 잡음, 음원의 이동이나 해수면의 거칠기에 의한 도플러 효과 등이 있다.[1] 또한 전송 거리가 증가할수록 대역폭이 줄어들어 데이터의 전송효율이 떨어진다. 이러한 수중음향통신 환경에서 해저, 해수면, 수심 등의 시공간 변화에 의해 다중 경로 전달 특성이나 도플러 확산이 성능에 영향을 미치므로 시스템 설계 시 이를 극복할 수 있는 채널 부호화 및 변·복조 기술은 성능을 좌우하는 아주 중요한 기술들이다.[2] 채널 전달 특성 등의 환경이 매우 빠르게 변하는 수중음향통신 환경에서 지상 시스템에서와 같이 고정적인 채널 부호화 및 변·복조 방식의 적용 보다는 이러한 환경에 적응적으로 서로 다른 부호화율 및 변·복조 방식들이 변화하는 적응형 부호화 변조 기법 Adaptive Modulation and Coding(AMC)은 다양한 수중 채널 환경을 극복하면서 전송 거리를 더욱 확장함과 동시에 성능을 보장하는 기법이다.[3,4,5,6,7] AMC 기법은 수중 통신 채널에 적합한 부호화율과 변조 방식을 조합한 여러 모드 중 오류율이 낮은 최적의 모드로 전송한다. Reference [8]에서는 송신단에서는 Ready to Send(RTS) 신호를 전송하면 수신측에서는 채널 상태 정보를 담은 Clear to Send(CTS) 신호를 송신측에 보내어 송신측에서는 이러한 정보를 이용하여 부호화율과 변조방식을 조합한 적합한 모드를 선택하는 방식이다. 수중 채널 상태에 따라 수신측에서 송신측으로 전송 모드를 피드백하여 이에 따른 송신측에서는 해당되는 모드를 전송하는 방식이다. 그러나 수중 통신에서 은밀성의 측면으로 볼 때는 으로 인해, 즉 적에게 수중체등의 위치를 노출당하는 것을 방지하기 위해 역방향 채널 즉 피드백 정보는 전송하지 않기 때문에 동일한 정보를 2가지 모드로 설정하여 연접하여 전송하면 수신측에서는 수신 Signal to Noise Ratio(SNR)을 이용하여 두가지 모드 중 하나를 택하게 된다.[9,10] 따라서 본 논문에서는 잠수함등과 같은 수신측에서는 위치 탐지등의 은밀성을 유지하기 위해 송신측으로 어떠한 피드백 정보 없이 송신측에서 여러 모드의 조합을 전송하여 성능이 가장 좋은 모드를 선택하여 복조 및 복호를 한다고 가정한다. 본 논문에서는 데이터 전송률과 변조 방식이 다른 네 가지 전송 모드를 적용하여 분석 한다. 동일한 정보 비트에 대해 다른 정보량을 가지는 네개의 다른 모드가 송신기에서 패킷으로 전송되며, AMC 시스템의 중요한 점은 어떤 모드가 최상의 성능을 갖는지 찾는 것이며 본 논문에서는 적절한 모드를 결정하기 위한 임계값 검출 알고리즘을 제시한다. 여기서 각 모드에 대한 식별은 각 패킷의 시작점에 각 모드에 해당되는 서로 다른 프리앰블 혹은 고유의 비트를 첨가하여 수신측에서는 상관도를 이용하여 다음 데이터가 어떤 모드로 동작하는지 식별한다. AMC 실험은 2019년 5월 경북의 한 호수에서 서로 다른 거리에서 수행되었다. 임계값 검출 알고리즘을 기반으로 네 가지 모드의 성능을 분석 하였다.
II. AMC 송수신모델 및 임계값 검출 알고리즘
2.1 AMC 송신부 모델
시변동성이 높은 수중 채널 환경에서의 통신을 위한 적응형 전송 방식 중 다양한 채널 부호기의 부호화율 R과 MPSK 변조 방식의 M의 다양한 모드의 조합을 이용한 AMC 전송 방식은 Fig. 1의 송신부 모델과 같이 시변 수중 채널 특성에 적합하도록 채널 부호화의 부호화율 R과 변조 지수 M의 조합하여 전송하는 방식이다.
채널 부호화기의 부호화 기법은 컨볼루션 부호화기법을 이용하였으며,[11] 이는 입력 비트의 길이가 자유롭게 설정 가능하기 때문이다. 컨볼루션 부호화기를 통과하여 출력된 부호화된 비트는 연집오류를 산발 오류로 만들어 복호 성능을 향상시킬 수 있도록 부호화된 비트의 순서를 다르게 하는 과정을 거친다. Table 1과 같이 송신신호는 각 모드에 따라 부호화율 및 변조방법을 달리하여 송신신호를 생성한다.
Table 1.
Mode parameters.
| Mode | Input K | Coding rate | Modulation method | Symbol size |
| 1 | 40 | 1/3 | BPSK | 120 |
| 2 | 80 | 1/3 | QPSK | 120 |
| 3 | 60 | 1/2 | BPSK | 120 |
| 4 | 120 | 1/2 | QPSK | 120 |
위의 표와 같이 각 모드에서 출력되는 심볼의 길이는 동일하게 설정하며, 부호화기 입력 비트 수를 다르게 하였다. 부호화율이 작을수록 입력 비트의 수는 작으며, 클수록 많은 정보 비트를 전송한다. 따라서 채널 환경이 좋을 때는 많은 정보를 전송할 수 있으며, 열악할 때는 적은 정보를 전송하여 안전하게 복호 가능하게 한다.
2.2 AMC 수신부 모델
Table 1과 같은 모드를 이용하여 Fig. 2와 같은 수신부 구조로 설계 하였다. 수신부에서는 성능을 향상시키기 위하여 BCJR 디코더와 터보등화기법을 적용하여 설계하였다.[12,13] 수신된 신호는 아날로그/디지털 변환을 거쳐 패킷 동기를 획득한 후 어느 모드에서 오류가 적은지 네 가지 모드 중 하나를 선택하기 위해 임계값을 결정한다.
2.3 임계값 결정 파라메타 검출 기법
임계값 결정 파라메타는 적응형 전송 방식에서 다중 모드 중 어느 모드가 오류가 가장 적은지, 성능이 가장 좋은 모드를 선택하는데 있어서 가장 중요한 요소 기술이다. 본 논문에서는 아래와 같은 세 가지 방식을 설정하여 세 가지 방식의 값을 종합적으로 분석한 후 결정한다.
2.3.1 ESNR(Effective SNR) 추정 방식
ESNR 방식은 송·수신간에 서로 알고 있는 보조 신호 또는 사전 신호로 사용한 의사 잡음 신호를 이용하여 수신단에서 수신 SNR을 추정하여 추정된 SNR과 채널 부·복호 알고리즘의 비부호화 오류율의 상관도를 이용하여 채널 부호화 알고리즘의 Quassi Error Free(QEF) 조건을 만족하도록 임계값을 설정하는 방식이다. QEF란 통상적으로 복호 후 오류율이 매우 낮은 영역을 의미한다. 통산적인 시뮬레이션의 경우 입력 SNR에 따른 부호화율 및 변조 방식에 따라 BER 성능 곡선을 산출하지만 호수 및 해상 실험에서는 수신 SNR 에 따라 성능 곡선을 산출해야 하므로 수신 SNR을 산출하기 위해서는 Fig. 3과 같이 데이터를 보내지 않는 패킷의 일정한 침묵 구간에서 잡음 전력을 구하고 수신된 신호의 전력과의 상관성을 이용하여 수신 SNR을 구한 후 이에 따른 비부호화 오류율과의 상관성을 이용하여 결정하는 방식이다. 수신 SNR을 측정하기 위해서는 수신신호의 침묵 구간과 PN 구간을 사용하여 Eq. (1) 과 같이 계산 된다.
여기서 은 송수신간의 서로 알고 있는 수신된 PN 신호의 전력이며, 은 수신된 사일런스 구간에서의 잡음신호를 나타낸다. 사일런스 구간에서는 신호가 전송되지 않는 보호 대역 구간으로 이 구간에서 잡음 신호의 전력을 구하며, 데이터 구간에서는 신호와 잡음이 모두 합쳐 수신되므로 이 구간에서는 신호와 잡음이 합친 전력을 구하여 Eq. (1)과 같이 수신 SNR을 산정한다.
2.3.2 PES(Post-Equalization SNR) 추정 방식
PES 방식은 수신단에서 Least Mean Square(LMS) 또는 Recursive Least Square(RLS) 방식을 적용하는 등화기에서 수신신호와 등화기의 출력의 차이인 오류 성분을 측정하여 ESNR 방식과 마찬가지로 채널 부호화 알고리즘의 QEF 조건을 만족하도록 임계값을 설정하는 방식이다. 이는 잡음 전력 보다는 다중 경로로 인한 간섭량에 따른 임계값을 설정하는 방식이므로 다양한 다중 경로에서 실제 시스템에서는 정확하지 않을 수 있다.
2.3.3 PN 오류율 상관관계 추정 방식
수중 통신에서 데이터를 전송하기 위한 패킷의 구조는 처음 동기 획득을 위해 데이터 전송 전에 PN 시퀀스를 데이터의 헤드 부분에 패킷화 하여 전송한다. PN 신호는 송수신간에 서로 알고 있는 데이터를 이용하여 동기를 획득하는 기능을 하고 있으므로 채널 부호화를 하지 않고 전송된다. 이러한 비부호화 된 PN 데이터는 대부분의 연구에서는 동기 획득을 위해 활용되지만 이의 성능을 이용하여 데이터 부분의 성능 또한 예측할 수 있어 데이터 부분의 복호 부에 정보를 제공할 수 있다. 기존의 연구는 PN의 역할이 데이터 부분의 주파수 및 위상 동기를 획득하기 위해 적용되었다. 그러나 다중 경로 등의 열악한 채널 환경에서는 PN의 비트 수를 수십 ~ 수백 비트로 할당하므로 이의 오류율 또한 데이터 부분의 오류율과 상관성을 가지고 있으므로 비부호화 된 PN의 오류율을 이용하여 데이터 부분의 오류율을 예측하여 데이터 부분의 복호 후에 QEF 조건을 만족하도록 임계값을 설정하는 방식이다.
2.3.4 터보 등화 구조
음파를 이용하는 수중 통신 채널에서 다중 경로 전달 특성으로 인해 수십 [ms] 정도의 지연확산 현상이 발생하는 수중 통신에서 채널 부호화 기술만으로 만족할만한 성능을 향상시키기가 힘들다. 따라서 채널 부호화 기법과 함께 등화기 기법을 적용하여 복원하는 연구가 이루어지고 있다. 과거 대부분의 연구에서는 등화기와 채널 부호화 기법을 서로 별개로 적용함으로써 성능 개선에 한계를 나타내었다. 수신단에서 등화기와 채널 복호기 사이에 반복적인 연산 과정을 통해 심벌 간 간섭을 크게 줄일 수 있는 터보 등화기에 대한 연구가 이루어지고 있다.[13]Fig. 1과 Fig. 2에서 데이터는 반복 부호화기를 거치고 난 뒤 인터리버, 심벌 매핑 후 변조기를 통과하여 전송한다. 전송된 심벌은 채널을 통과한 후 백색 가우시안 잡음이 더해진다. 수신단의 터보 등화기는 등화기와 반복 복호기로 구성되어 있으며, 등화기와 복호기는 인터리버와 역-인터리버를 통해 연결되어 서로의 정보를 반복해서 갱신한다. 인터리버는 송신측에서 한 개 블록 크기의 부호기 출력 값을 재배치시키고, 역-인터리버는 인터리버의 역 과정을 거쳐 송신신호를 복원한다. 복호기에서 출력한 피드백 정보는 다시 인터리빙 과정을 거쳐 정정된 신호를 각 밴드의 등화기에 재입력한다. 이러한 인터리빙 과정은 다중 채널 환경에서 수신된 신호의 밀집된 오류를 분산 시키는 역할을 하게 되어 성능을 향상 시킨다. 송신된 신호는 수중채널을 거치고 백색 가우시안 잡음이 더해져 수신된다.
Fig. 2에서 기저대역으로 변환한 후 는 결정 궤환 등화기의 출력 값으로 수신 신호로부터 등화기에서 추정되어진 외부 정보 값이다. 수중 채널의 심볼간 간섭이 첨가된 수신신호를 시점에서의 등화기 입력 값이라 하면, 값은 결정 궤환 등화기의 출력 값 와 의 차를 역-인터리빙하여 복호기로 입력한다. 복호기에서 추정되어진 외부 정보 값은 이며, 이는 복호기의 출력 값으로써 사후 확률 값을 계산하여 0 또는 1의 오류 값을 보정할 수 있는 값이다. 이러한 와 의 차이 값을 인터리빙한 가 결정 궤환 등화기에 입력된다. 를 업데이트 하여 오류 값을 보정하는 방법을 취하게 되는데, 반복횟수가 늘어남에 따라 업데이트 하는 오류 보정 값이 송신하고자 하는 원 신호에 가깝게 되어 성능이 향상된다.
III. 실험결과
본 논문은 2019년 5월 경북 한 호수에서 Table 2와 같은 파라메타를 설정하여 수중실험을 진행하였다. 실험은 송수신기 사이의 거리를 다르게 하여 100 m, 250 m, 400 m의 거리에서 실험하였으며, 호수 깊이 45 m에서 송신기는 3 m, 수신기는 35 m에 두고 실험을 하였다. 이는 실험 전 송수신기 위치에 대한 데이터 전송 실험을 하여 최적의 위치를 선정하였다. 송신신호의 중심주파수는 16 kHz, 샘플링 주파수는 192 kHz로 설계하였다. Source는 Table 1과 같이 가변적으로 40 bits ~ 120 bits로 하였으며, 각 모드별로 부호화율과 변조 기법을 다르게 설정하였다. 거리는 각 모드에서 성능 한계를 알아보기 위해 100 m에서 점점 멀어지게 하여 400 m까지 이동하여 각 지점에서 성능을 산출하였다.
Table 2.
Experiment parameters.
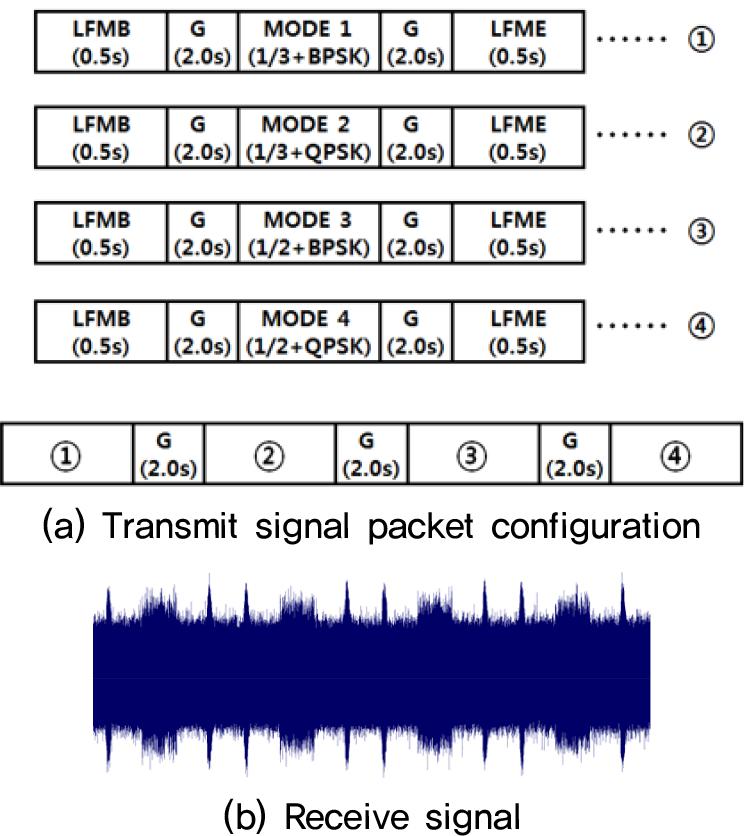
위의 그림은 네 가지 모드에 대한 송신 신호 패킷 구성과 수신 신호를 나타낸다. 송신 신호의 패킷 구성은 Fig. 4(a)와 같이 각 모드별로 패킷을 구성하고, 모드별 패킷 사이에 gap(2 s)을 주어 전체 패킷을 구성하였다. 가장 먼저 1 s 동안 Linear Frequency Modulation Begin(LFMB) 신호를 보내고 2 s 동안 사일런스 구간을 두고 다음 mode 신호, 침묵 구간, 마지막으로 Linear Frequency Modulation End(LFME) 신호로 구성되어 사이에 2 s의 사일런스 구 간을 두고 모드1, 모드2, 모드3, 모드4 순서대로 송신신호를 구성하였다. Fig. 4(b)는 수신 신호의 파형을 나타내며, 각 모드별 LFMB와 LFME이 구분됨을 알 수 있으며, LFMB를 이용하여 각 모드의 시작점에 대한 동기를 획득하고 PN 신호를 분석하여 각 모드의 임계치 측정값을 분석한다.
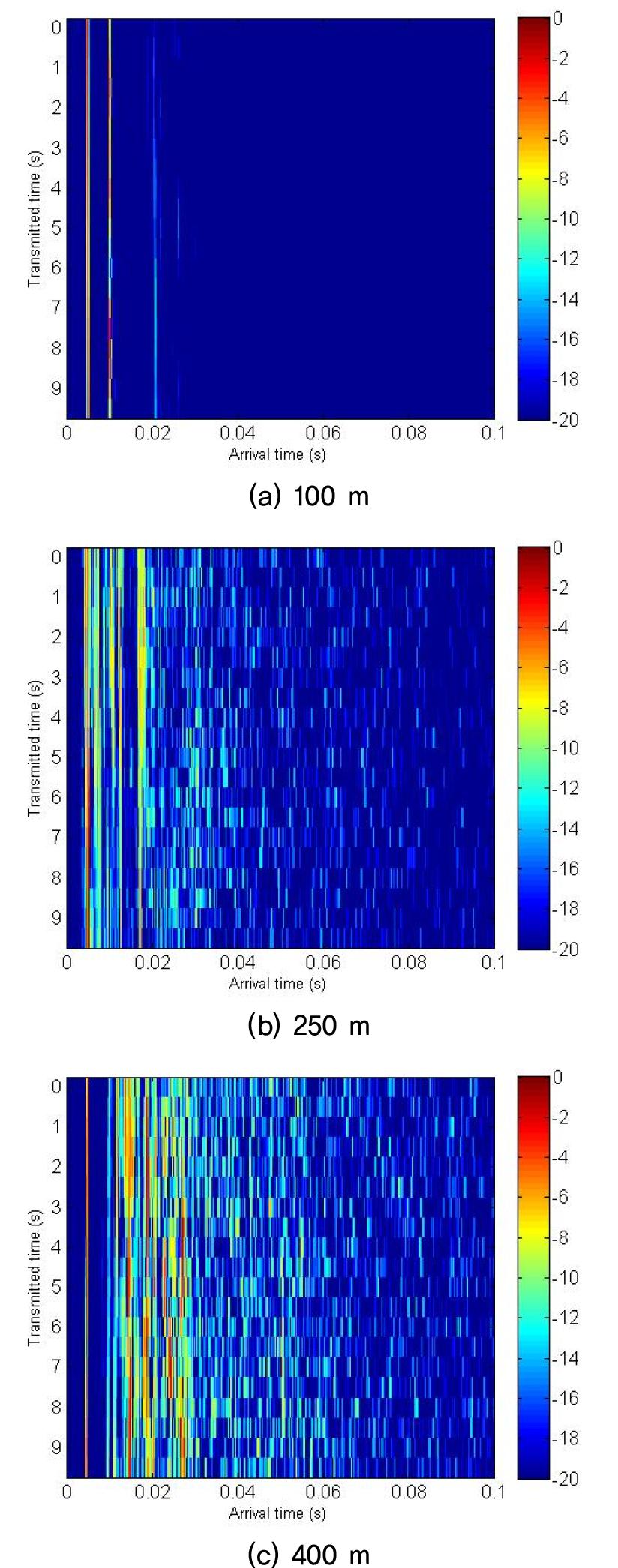
Fig. 5는 거리에 따른 Channel Impulse Response(CIR)를 나타낸다. 그림에서 알 수 있듯이 거리가 멀어짐에 따라 수중 채널 환경이 열악한 것을 알 수 있으며 다중경로의 경우 100 m에서는 직접파 이후 매우 약한 신호의 다중 경로가 있었으며, 250 m와 400 m의 경우에는 직접파 이후 매우 강한 신호의 다중경로가 한 개 이상 존재하는 것을 알 수 있다.
Table 3은 네가지 모드에 대한 각 거리에서의 실험결과를 나타내고 있다. ESNR은 Fig. 3과 Eq. (1)을 바탕으로 구한 수신 신호의 SNR을 의미하며, PES는 등화기의 오차 분산, Data BER은 복호 후 최종 오류율을 의미한다. Table 3에서 100 m 에서는 모든 모드에 대하여 Data BER이 0이 되는 것을 알 수 있다. 250 m 에서는 모드 1과 모드 2에서 그리고 400 m 에서는 모드 1에서만 Data BER이 0이 되었으며 최고의 성능을 나타내는 것을 알 수 있다. 거리가 멀수록 수신 SNR을 나타내는 RSNR은 점점 감소됨을 알 수 있으며, 수신신호와 PN 신호의 오차를 나타내는 PES는 점점 증가되는 것을 확인할 수 있다. PN 비트의 BER은 데이터 부분의 BER을 나타내는 척도로써, PN 오류율이 이하이면 데이터 부분의 오류를 모두 수정 가능함을 알 수 있다. 따라서 성능 한계를 분석시에 모드 1을 예를 들면, 송수신 거리가 100 m, 250 m, 그리고 400 m일 때, ESNR이 0.75[dB] 이상, PES는 0.36이하 PN 오류율이 이하이면 데이터 오류가 모두 수정됨을 알 수 있다. 위의 표에서 네가지 모드를 수신하였을 때, 어느 모드가 오류가 가장 적은지에 대한 척도는 세가지 임계값 검출 알고리즘에서 PN 오류율이 가장 적합함을 알 수 있다.
Table 3.
Experimental results for four modes.
IV. 결 론
수중음향통신 채널은 직접파와 더불어 해수면과 해저면의 반사 등으로 인해 다중경로 전달을 포함한 다양한 특성 및 거리에 따른 전달 손실로 성능 저하를 일으키며 음파가 전달되는 형태가 복잡하다. 이러한 다양한 채널에서 송수신간의 데이터 전송시 채널에 적합한 통신 방식이 적용되어야 한다. 따라서 시변동성이 높은 수중 채널 환경에서의 통신을 위해 채널 환경에 따라 채널 부호화기의 부호화율, 변조 방식등을 다르게 적용하여야 하는 적응형 전송 방식의 적용은 필수적이다. 적응형 전송 방식 중 다양한 채널 부호기의 부호화율 R과 MPSK 변조 방식의 M의 다양한 모드의 조합을 이용한 적응형 부호화 변조 기법은 열악한 채널에서는 전송 효율은 손해를 보더라도 성능이 우수한 부호화율이 낮은 채널 부호화기 및 변조 방식이 선택되어야 하며, 채널 상태가 양호할 때는 비록 성능은 낮지만 전송 효율이 높은 조합을 선택하여야 한다. 따라서 채널 상태에 따라 데이터 복구 성능이 우수한 조합을 선택하기 위해서는 각 조합에 대한 임계값을 설정하여 복원해야 한다. 따라서 본 논문에서는 은밀성을 위해 수신측에서 피드백 되는 정보가 없다고 가정하여 네 가지 모드를 구성하여 호수 실험을 통한 각 모드에 대한 성능을 만족하는 임계값을 설정하였다. 실험 결과를 통하여 각 모드에 따른 데이터 BER의 성능을 기반으로 계산된 세 가지의 임계값 설정 알고리즘, 즉 ESNR, PES, PN 오류율 등에 대해 분석하였다. 세가지 모드를 거리별로 분석한 결과 PN 오류율이 모드를 선택하기에 가장 적합한 방식임을 알 수 있다. 이는 지상 통신과는 달리 수중에서 별도의 채널 추정 및 수신부에서의 부가적인 피드백 정보를 사용하지 않아도 최적의 성능을 가지는 모드를 결정할 수 있을 것으로 사료된다.