I. 서 론

수중 이동체를 개발하고 성능을 분석함에 있어서 이동체의 위치를 추적하는 것은 반드시 필요한 과정이지만 지상에 비해 많은 어려움이 있다. 이러한 수중 이동체의 위치 추적을 위해 일반적인 능동 및 수동형 소나가 아닌 이동체에 핑어(pinger)를 장착하고 관측소에서 이 신호를 수신하여 위치를 추적하는 방법이 연구되었다.^[1] 하지만 이러한 방법은 2차원 공간에서의 위치 추적이며, 이동체의 위치를 3차원 공간에서 추적하고자 하는 경우 원칙적으로 수신기들의 배치를 3차원 공간으로 구성해야만 한다. 이에 반해 이동체에서 심도 정보를 직접 측정하고, 측정된 정보를 핑어에 보내어 위치 추적을 위한 송신 핑(ping)과 함께 전송한다면 관측 수신기들의 배치를 3차원이 아닌 2차원적으로 수월하게 구성할 수 있는 장점이 있다. 측정된 심도 정보를 전송하기 위해서 위치 추적을 위한 핑과의 조합된 신호 구성을 가지며, 수중음향통신 기법을 이용하여 심도 정보만 전송하면 되기 때문에 데이터 양은 많지 않다. 하지만 핑어가 부착된 이동체가 고속으로 이동하는 경우도 있기 때문에 도플러 주파수 변동성이 매우 큰 환경이 되어 수신단에서 정확한 심도 정보를 추정하기 어렵게 한다. 특히, 음파의 경우 주파수가 전자기파에 비하여 매우 낮기 때문에 도플러 천이 효과에 취약하고, 천해에서는 해수면과 해저면 등에 반사된 다중 경로 전달 현상이 존재한다.^[2] 수중 이동체가 수신기로부터 멀리 떨어져 있는 경우 도플러 천이 주파수가 비교적 일정하지만 수신기 위치를 기준으로 근접한 지점을 지나는 경우 천이되는 도플러 값이 시간에 따라 급변할 수 있다.^[3]

도플러 변동성이 큰 환경에서 전송된 정보의 복구를 위해서는 도플러 영향의 보정이 필요하다.^[4] 보정을 위한 기존의 방법 가운데 하나는 도플러 뱅크를 통해 많은 수의 리플리카를 이용하여 수신 신호와의 상관도를 구해 최대치를 나타내는 값으로 도플러 주파수를 추정하고 추정치를 정보를 복구할 때 적용하는 것이다.^[5] 앞과 같은 도플러 뱅크 방법은 생성되는 리플리카들 사이의 주파수 간격이 좁아질수록 성능이 좋아지는 장점이 있지만 상대적으로 계산량이 증가하면서 동작시간이 길어지는 단점이 존재한다.

모의실험 이전에 일정한 영역 안에 다수의 수신기가 존재하며 그 안을 송신기가 통과하는 상황을 가정하여 신호 대 잡음비는 10 dB이상이 유지된다고 가정하였다.

본 논문에서는 도플러 천이 변동성이 큰 환경에서 기존의 도플러 뱅크를 이용하는 방법보다 적은 계산량으로도 성능을 갖도록 하는 방법에 대해 연구하였다. 적용한 방법은 도플러 천이 주파수 추정을 위한 리플리카 수를 줄이는 대신에 시간 축에서 보정하도록 하여 동기화 과정을 추가 수행하였다. 연구된 방법은 모의실험을 통하여 성능을 분석하였다.

II. 심도 정보 전송을 위한 패킷 구성

먼저 심도 정보 전송을 위한 신호는 다음 Fig. 1과 같이 M-bit 심도 정보가 먼저 존재하고 바로 뒤에 N-bit의 위치 추적용 신호가 이어지는 형태로 구성되어 있다. 위치 추적용 신호는 Target Identification(TID)를 사용하며 송신기마다 직교성을 갖는 코드들로 구성 된다 . 심도 정보는 채널 부호화 기법을 사용하여 실제로는 L개의 비트를 가지게 된다.

Fig. 1.

Packet structure.

도플러 주파수 천이 환경에서는 일반적인 위상천이 변조 방식(Binary Phase Shift Keying, BPSK)은 복조과정에서 절대적인 위상만을 이용하는데 반해 차동 위상 편이 변조 방식(Differential Phase Shift Keying, DPSK)의 복조에서는 심볼과 심볼간의 위상차만을 이용한다. BPSK 변조방식은 도플러 효과 등에 의해 위상 변화가 존재한다면 위상 변화가 누적되며 기준위상에서 큰 오차가 발생하게 되지만 DPSK 변조방식은 비슷한 위상오차가 발생하여도 인접 심볼간의 위상차만을 이용해 위상 오차가 누적되지 않기 때문에 도플러 환경에서 더 유리하게 작동한다.

DPSK 변조는 미리 값이 정해진 기준 비트를 시작으로 디지털 논리에서 사용하는 exclusive-OR(XOR) 인코더를 통과한 데이터를 사용한다.^[6] 심도 정보 신호에 이어지는 위치 추적용 신호는 의사 잡음 코드를 사용하며, 위치 추적용 신호 역시 DPSK 변조된다. 결국 위치 추적용 의사 잡음 신호는 심도 정보 신호의 시간 동기를 맞추기 위한 포스트 앰블의 역할을 하게 된다. 이렇게 구성된 전체가 하나의 핑 신호로 사용된다. 심도 정보는 Fig. 1에서 첫 번째 비트부터 앞쪽 방향으로 DPSK 변조가 이루어지고, 의사 잡음 신호는 첫 번째 비트부터 뒤쪽 방향으로 DPSK 변조가 이루어진다.

DPSK 변조 방식의 신호 생성은 일반적은 BPSK 변조 방식과 똑같으나 이진 수열 $b_i$가 DPSK 인코딩된 데이터라는 차이점이 존재한다. 따라서 생성된 신호는 아래의 식 Eq. (1)과 같다. 식에서 $s_f\left(t\right)$는 생성된 신호이고 $s_0\left(t\right)$는 DPSK 인코딩된 데이터 $b_i$가 0인 경우 생성된 신호, $s_1\left(t\right)$은 $b_i$가 1인 경우이다. $f_c$는 중심 주파수, $A$는 신호의 진폭을 의미한다.

핑은 1 s 간격으로 전송되며 수심 정보는 4번의 핑을 통해 전송된다. 예를 들어 전송해야 하는 수심 정보가 63 m일 경우 첫 번째 핑은 6 이라는 정보를 갖는 수심정보를 전달하고 2 ~ 4번째 핑은 3이라는 숫자를 전달한다. 4번의 핑 전달을 통해 전달하도록 설계를 한 이유는 초당 전송 가능한 심도 정보가 하나의 십진수만 전달이 가능하기 때문이다. 이 때문에 심도 정보의 변화가 작은 10 m 단위의 정보보다 1 m 단위의 정보가 더 크기 때문에 1 m 단위의 정보를 자주 전송했다.

III. 심도 정보 추정 과정

전송된 신호의 도플러 주파수 천이 효과는 송신기와 수신기 사이에 상대적인 속도가 존재할 때 발생하게 된다. 송신기와 수신기 사이에 상대적인 속도가 존재하면 신호가 도착하는 시간이 변화하게 되며 송신기와 수신기가 가까워지는 방향으로 이동하는 경우 신호의 시작부분이 도달하는데 걸리는 시간과 신호의 마지막 부분이 도달하는데 걸리는 시간이 서로 다르며 마지막 부분이 더 빠르게 도달하므로 신호가 압축된다.^[7] 반대로 송신기와 수신기가 멀어지는 경우 신호의 시작부분 보다 마지막 부분이 도달 하는 시간이 오래 걸리므로 신호는 팽창된다. 도플러 천이 주파수는 송수신기 사이의 상대 속도가 $v$일 경우 다음의 식과 같이 표현할 수 있다.

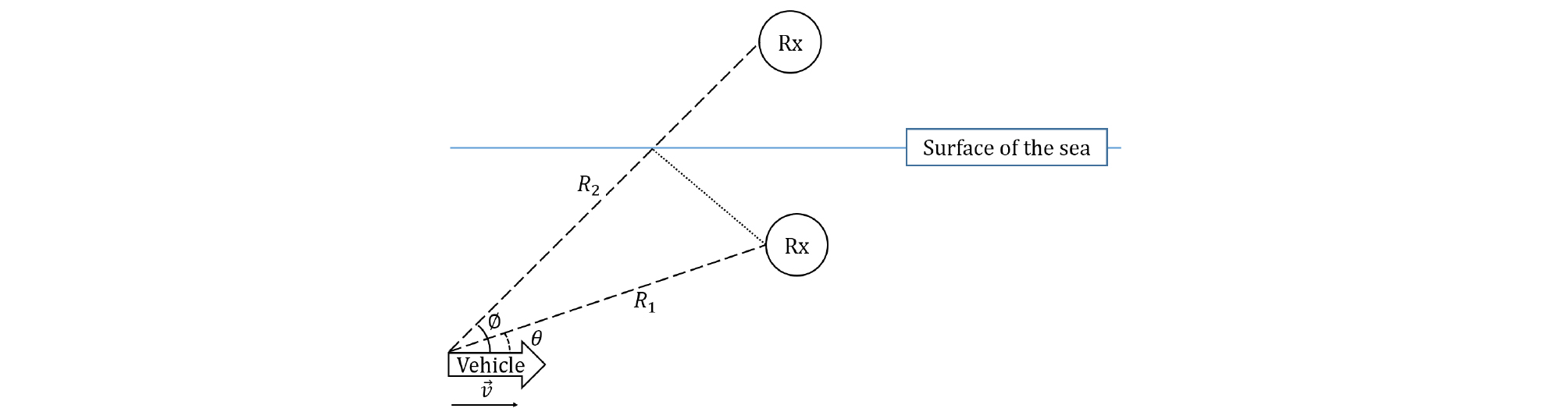
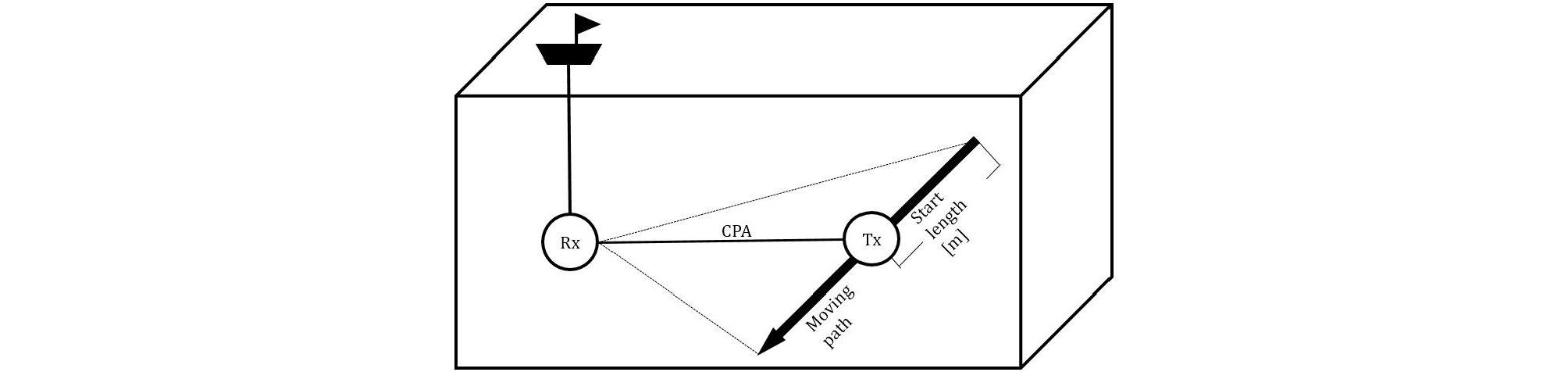
Eq. (2) 에서 $\theta$는 Fig. 2와 같이 고정된 수신기가 이동하는 송신기와 이루는 각도이며 $f_d$는 도플러 주파수, $f_c$는 중심 주파수 그리고 $c$는 음속을 의미하며 본 문에서는 1500 m/s로 가정하였다.

Fig. 2.

(Color available online) Geometry between underwater vehicle and receiver.

Fig. 2는 이동체와 수신기 사이의 직접 전달경로뿐만 아니라 해수면에 의한 반사 신호도 표현하고 있다. 반사 신호는 그림과 같이 해수면을 기준으로 거울과 같은 형태의 배치로 생각할 수 있으며, 이를 이용하여 각도 $\varphi$를 찾고, 이에 따른 반사 신호의 도플러 천이 주파수도 계산할 수 있다.

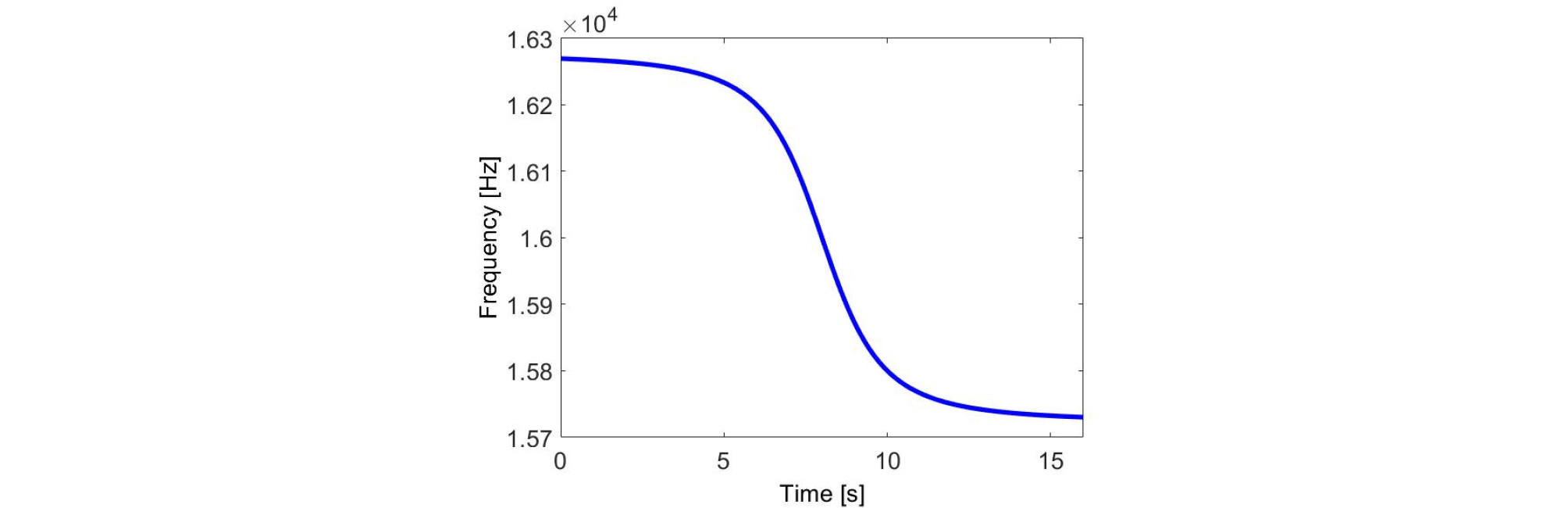
이동체의 속도가 50 kn이며 Closest of Point Approach (CPA)가 50 m 떨어져 있고 중심 주파수가 16 kHz 일 때 도플러 천이 주파수의 변화는 Fig. 3과 같이 나타난다. 시뮬레이션은 총 16개의 핑이 전송되며 전송될 때 직접 경로로 전달되어 수신된 신호 $r_d\left(t\right)$는 아래와 같이 표현된다.

Fig. 3.

(Color available online) Carrier frequency variation by Doppler effect.

Eq. (3)은 도플러 천이된 수신신호로 ${\theta }_0$는 채널의 의한 위상 천이를 의미한다. Eq. (3)은 Eq. (4)와 같이 이동 변화하는 것을 나타낼 수 있으며, 이 식들을 정리하면 Eq. (5)와 같아진다.

Eq. (5)에서 ${\alpha }_d$는 첫 번째 경로로 도달하면서 생기는 감쇄, $\theta$는 이동하는 경로와 실제 수신기로 진행하는 음원이 이루는 각도, $R_1$은 음원이 첫 번째 경로를 통하여 수신기까지 도달하는데 걸리는 거리이며 송신기가 이동함에 따라 값이 변하게 된다. $w\left(t\right)$는 백색 가우시안 잡음이다. Eq. (6) 는 해수면을 맞고 반사되는 신호 $r_s\left(t\right)$에 대한 것으로, ${\alpha }_s$는 감쇄, $\varphi$는 $\theta$와 같은 요소이며 $R_2$는 Fig. 2와 같이 나타난다.

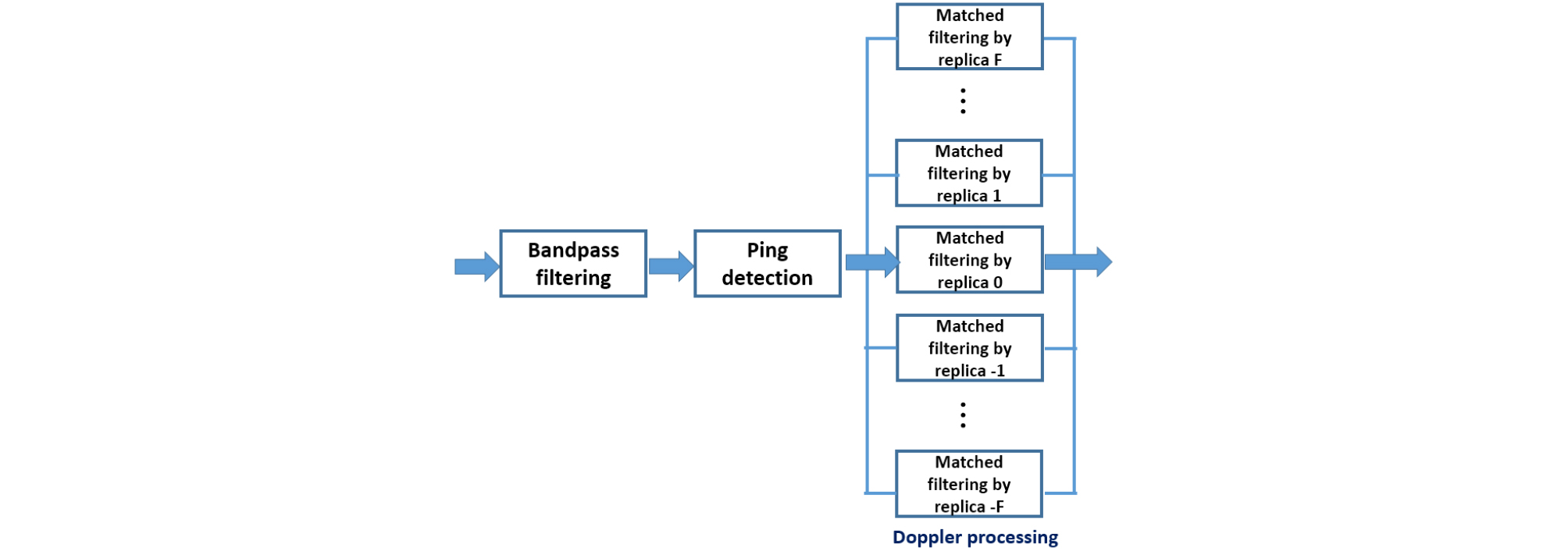
심도 정보 데이터 신호의 포스트 앰블 역할을 하는 위치 추적용 신호 또한 도플러 주파수 천이 영향을 받아 신호의 길이가 압축 또는 팽창 변화하면서 시간 축에서 신호의 위치도 변한다. 수중 이동체로부터 전송된 심도 정보를 복구하기 위해서 본 논문에서는 2단계에 걸친 주파수-시간 동기화 기법을 적용하였다. 이 때 2차 시간 동기화 기법은 기존의 통신 프레임 동기화를 위해 연구된 방법^[8]을 적용하였다. 먼저 에너지 검출기를 이용하여 신호가 존재하는 대략의 위치를 찾은 다음, 대략적인 위치를 이용하여 신호를 일부분만 자른다. 에너지 검출기를 통해 탐색된 신호를 사용하여 도플러 뱅크내의 리플리카들과 상호 관계를 확인한다. 이 때 각 리플리카들 사이의 주파수 간격은 기존의 것보다 넓게 설정하여 상호상관도를 구하기 위한 계산량을 감소시킨다. 리플리카는 Fig. 4에 나타낸 것과 같이 중심 주파수를 기준으로 위로 $F$ 개 아래로 $F$ 개 총 $2\times F+1$개이며, 이로부터 대략의 주파수 동기점을 찾는다. 이 방법은 Fig. 4에 블록도로 나타내었다. 기존의 방법과 다른 점은 리플리카들 사이의 주파수 간격은 기존의 것보다 넓게 설정하였기 때문에 주파수 해상도가 낮다.

Fig. 4.

(Color available online) Block diagram of Doppler bank.

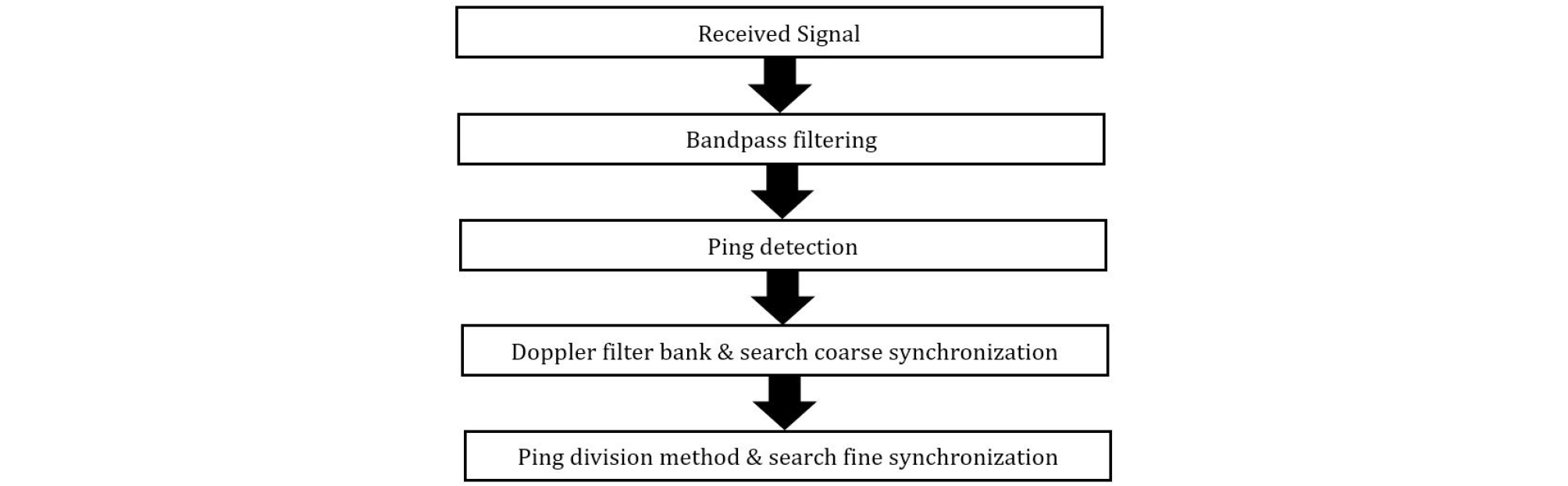
제안한 방법은 도플러 뱅크내의 리플리카들과 상호 관계 확인 과정 후에 시간 동기화를 한 번 더 수행한다. 위 과정을 추가한 이유는 의사 잡음 신호가 전송되는 동안 도플러 천이 주파수가 변하였다면 추정된 도플러 천이 주파수를 이용하여 찾은 동기가 정확하지 않을 수 있다. 그러므로 신호의 시작점을 보다 정확하게 찾기 위해 핑 신호를 분할한 뒤 일부만 사용하여 시간 동기를 재탐색하도록 하였다. 그리고 재탐색된 동기를 이용하여 심도 데이터를 복조하게 된다. Fig. 5에 제안한 방법에 대한 흐름도를 나타내었는데 먼저 수신된 신호를 대역 통과 필터에 통과시켜 핑 신호 이외의 잡음들을 제거한다. 다음에 핑을 찾을 때는 송신한 위치 추적용 신호와 상호상관관계를 구한 뒤 임계값 이상의 결과를 핑으로 인식한다. 그 뒤 대략 찾은 핑의 위치에서 넓은 도플러 주파수 간격의 리플리카와 상호상관관계를 통해 대략적인 도플러 추정이 이루어진다. 그 뒤 제안한 방법이 사용되는데 먼저 송신한 위치 추적용 신호의 1/2 혹은 1/4만을 가져오고 가져온다. 가져온 일부 신호는 추정된 도플러로 보간법을 통해 가져온 일부 신호에 도플러를 심어준다. 마지막으로 도플러가 심어진 가져온 일부 신호와 수신된 핑의 상호관계를 이용해 핑의 시작점을 재탐색 한다. 이때 신호의 앞부분을 가져오는데 이는 훈련신호의 앞부분에 심도 정보가 붙어있기 때문이다. 모의실험에서는 훈련 신호의 1/2을 사용하였다.

Fig. 5.

Procedure for data packet synchronization.

IV. 모의실험 및 결과

제안한 방법의 성능을 분석하기 위해 모의실험을 수행하였다. 심도 정보가 전송되는 비트 수는 7-bit가이다. DPSK 변조를 위한 기준 값은 “0”으로 하였으며, 기타 모의실험에 사용된 변수는 Table 1에 나타내었다.

Table 1. Simulation parameters.

모의실험은 수신기와 송신기의 심도를 모두 50 m 이며, 최근접 지점은 수신기로부터 50 m 떨어져 있는 경우를 가정했으며 모의실험에선 16개의 핑이 전송되며 신호 전송되는 시간의 중간 지점에 CPA를 통과하도록 설계되었다. 따라서 송신기의 전송 위치는 속도에 따라 변하도록 설계하였다. CPA 지점을 통과할 때 도플러변화가 가장 극심하고 이러한 경우 모의 실험결과를 얻었다. 위의 Fig. 6 시작 지점은 신호의 중간에 CPA 지점을 지나므로 50 kn(≒26 m/s)의 속도로 이동하는 경우 26 m/s × 8 s로 –208 m부터 208 m까지 이동하도록 모의실험이 설계되었다. 모의실험 상황에서 수심은 상대적으로 매우 깊다고 가정하여 해수면에 반사된 다중 경로 신호만을 고려했다. 두 번째 경로의 크기는 첫 번째 경로와 0.3배 차이가 나며 경로들마다 전달 과정에서 각도가 다르게 되므로 서로 다른 도플러 값이 적용됐다. 신호를 복조하는 과정에는 경로를 구분하지는 않았다. 경로를 구분하지 않아도 신호 복조시 에너지 검출기를 통해 핑의 위치를 찾고 도플러 뱅크내의 리플리카들과 상호 관계를 확인할 때 두 번째 경로의 크기는 첫 번째 경로에 비해 작기에 성능에 큰 영향을 미치지 않는다.

Fig. 6.

Geometry between underwater vehicle and receiver.

도플러 뱅크를 통해 추정된 값에 대한 보상은 보간법을 사용하였다. 먼저, 추정된 도플러 주파수와 실제 송신에 사용된 중심 주파수 사이의 비율을 추정한다. 다음으로 신호를 앞에 측정된 비율에 따라 팽창 혹은 압축하여 도플러에 대한 보상을 해주었다.

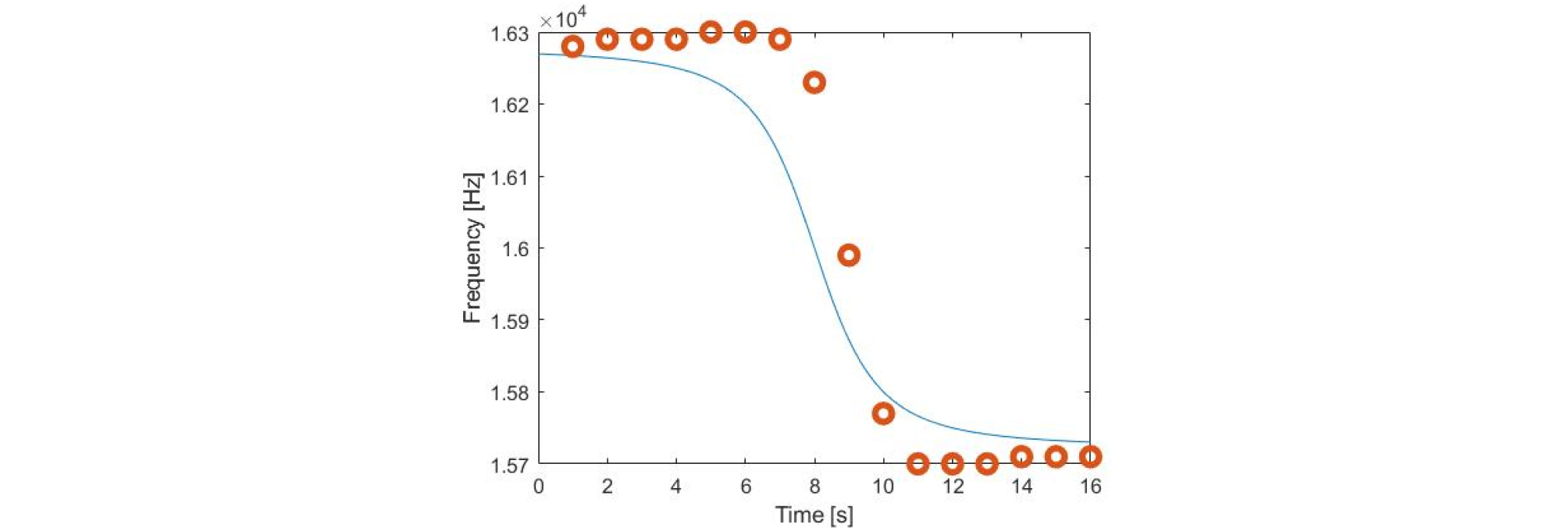
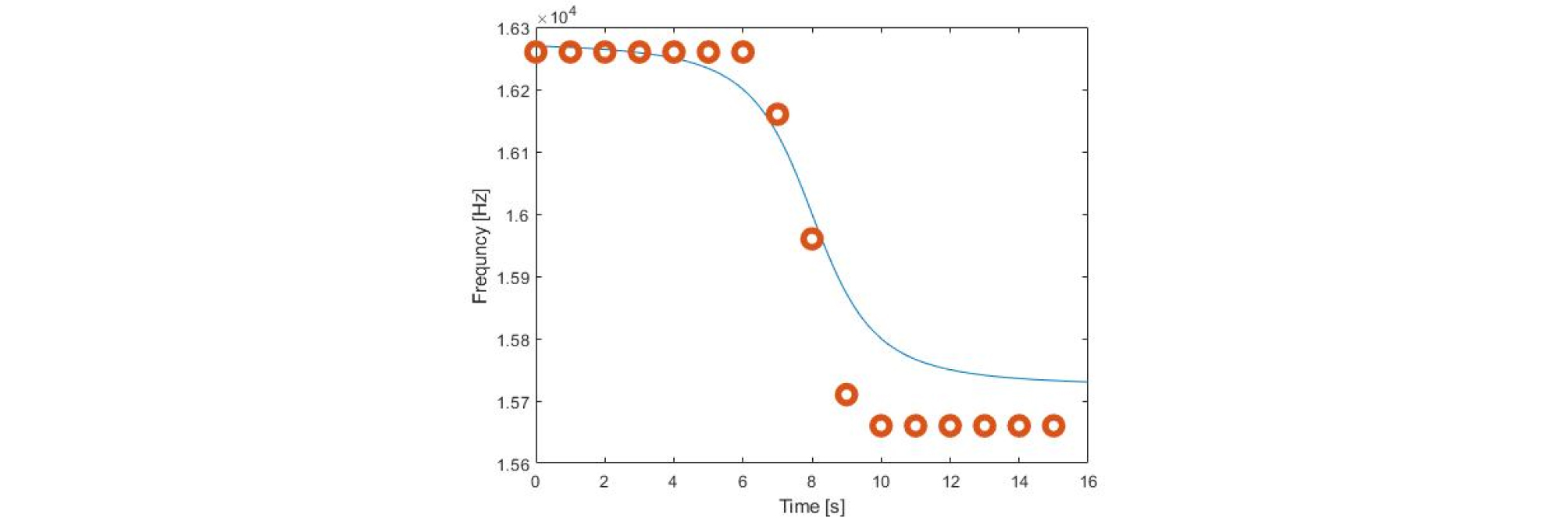
도플러 뱅크를 통해 추정된 값은 다음의 그림과 같이 나타났다. Fig. 7과 Fig. 8은 50 kn로 이동하는 표적에서 각각 10 Hz와 50 Hz의 간격으로 리플리카를 구성하여 추정한 도플러 값이다. 그림에서 파란색 선은 채널을 생성할 때 사용된 도플러 값이며 빨간 점이 도플러 리플리카를 통해 추정된 값이다.

Fig. 7.

(Color available online) Doppler frequency estimation [10 Hz interval].

Fig. 8.

(Color available online) Doppler frequency estimation [50 Hz interval].

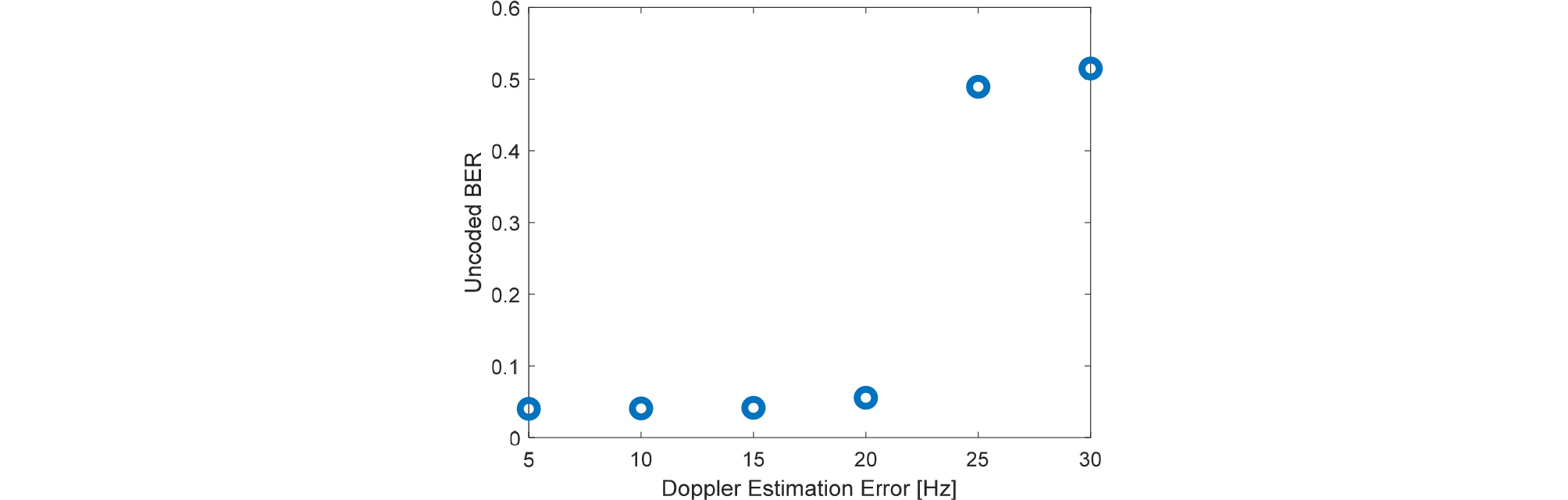
추정된 도플러 주파수와 실제 추정된 도플러 주파수 사이의 오차에 따른 오류 성능의 변화는 다음의 Fig. 9와 같다. 시뮬레이션은 50 kn로 이동하는 경우이며, 도플러 주파수 추정 간격은 25 Hz로 설정하였다. 그림의 x축은 추정된 도플러와 실제 추정된 주파수 차이의 절댓값이고, y축은 그때 비트 오류율이다. 추정된 도플러 값은 이동체가 이동하는 각 위치에서 2,000회 반복 수행하여 평균 오류율을 나타낸 것이다. 그림을 통해 도플러 주파수 추정 오차가 클 경우 전반적으로 오류 성능이 저하되는 것을 볼 수 있다.

Fig. 9.

(Color available online) BER performance according to Doppler frequency estimation error.

위와 같은 도플러 뱅크의 주파수 해상도에 따라 처리하는데 걸리는 동작시간과 비트 오류 사이의 관계에 대해 Table 2에 나타내었다. 시뮬레이션에서 이동하는 표적의 속력은 50 kn로 설정하였다. 제안한 방법을 사용하지 않고, 도플러 뱅크를 통해 주파수만 추정하여 심도 정보 신호를 보정하는 경우 20 Hz 이하의 간격으로 리플리카를 형성하였을 때 0.001 이하의 오류를 나타냈으나 30 Hz 이상의 간격을 가지면 오류율이 크게 증가하였다. 도플러 뱅크의 주파수 간격을 줄일수록 성능이 우수해지지만 프로그램의 동작시간이 증가하였다.

Table 2. Operating time according to Doppler resolution.

모의실험은 이동체 속도에 따라 이루어졌으며 10 kn, 30 kn, 50 kn로 이동하는 경우를 고려했다. 이 때 신호 대 잡음비는 10 dB로 설정하였다. 고속 이동체 환경에서 기존의 주파수만 추정하여 보정하는 방법과 제안한 방법으로 얼마나 정확하게 심도 정보를 전달할 수 있는지 다음의 Table 3에 나타냈다. 먼저 아무 보상도 해주지 않고 복조 하는 경우에는 모두 30 % 이상의 오류율을 나타냈다. 도플러 뱅크를 10 Hz 간격으로 형성하여 도플러 주파수를 추정하고 추정된 주파수만 보정하면 성능은 매우 우수하지만 앞서 언급한 것과 같이 계산량이 많아진다. 도플러 뱅크를 25 Hz 간격으로 형성한 뒤 도플러 천이된 주파수를 찾고 추정된 주파수만을 보상한 경우 6 % ~ 9 %의 오류율을 나타냈다. 그에 반해 논문에서 제안한 방법의 경우 도플러 뱅크 해상도는 25 Hz 간격으로 하는 대신 시간 영역에서 동기화 과정을 한 번 더 거치는 방식으로써 앞서 25 Hz 간격의 도플러 뱅크만을 이용하는 방법에 비하여 오류율이 0.2 % ~ 1 %로 나타나 성능이 향상되는 것을 확인할 수 있다.

Table 3. BER table of each case.

앞에 설명한 바와 같이 프로그램의 동작 시간 또한 굉장히 중요한 요소이므로 이를 Table 4에 나타내었다. 아무 보상이 없는 방법의 시간이 가장 짧으나 정보의 복조가 불가능하다. 25 Hz 간격을 갖는 리플리카를 적용하면 동작시간은 2.926 s이고, 제안된 방법이 적용된 경우 동작시간은 2.872 s로 차이가 미미하였지만 오류 성능은 크게 개선되었다. 모의실험에 사용된 컴퓨터의 사양은 Intel Core i7-7700K / 4.20 GHz CPU를 사용했으며 수신부의 시작부분에 Matlab의 내장함수 tic과 toc을 사용하여 연산시간을 측정하였다.

Table 4. Program operation time according to each method.

V. 결 론

이 논문은 도플러 천이 변동성이 큰 환경에서 기존의 도플러 뱅크만을 이용하는 방법보다 적은 계산량으로도 성능을 유지하는 방법에 대해 연구하였다. 적용한 방법은 도플러 천이 주파수 추정을 위한 리플리카 수를 줄이는 대신 시간 축에서 보정을 추가하였으며 시간 동기화를 위해 위치 추적용 신호를 분할하여 사용하였다. 모의실험을 통하여 제안한 방법의 동작시간은 비슷하나 성능이 개선되는 것을 확인하였다. 이후 실해역에서 취득한 데이터를 이용한 성능 분석이 필요할 것으로 보인다.