I. 서 론

최근 국내·외에서 선박을 이용한 해상물동량의 증가와 해상레저활동, 해상풍력단지 형성 및 연안개발과 같이 해상에서 인위적인 수중 소음을 유발하는 활동이 크게 증가하고 있으며, 이에 따라 수중 소음에 의한 어류의 집단 폐사, 해양 생물의 행동과 생리 변화와 같은 해양생태계 위협사례가 보고되고 있다^{[1], [2]}. 이로 인해 국제적으로 수중 소음을 규제하기 위한 방안이 제시되고 있으며, 주요 규제 대상 중 하나로 선박추진기가 언급되고 있다. 선박추진기의 주요 소음원 중 하나인 공동의 발생을 억제함으로써 공동 소음을 저감하기 위한 노력이 이루어지고 있으며, 군사적으로도 함의 생존성을 향상시키기 위해 공동 발생을 억제하는 저소음 추진기 개발을 위한 연구가 활발히 이루어지고 있다.

선박에서 발생하는 소음은 크게 엔진, 감속기어, 펌프류의 기계류 소음과 추진기 및 선체에서 발생하는 유동소음으로 구분할 수 있다. 유동 소음은 비공동 소음과 공동소음으로 구분하며, 비공동 상태에서는 추진기 소음은 날개 회전율 주기로 나타나는 Blade Passing Frequency(BPF) 성분과 난류에 의한 광대역 소음으로 나타날 수 있다.^[3] 추진기 공동소음은 광대역에 급격한 소음증가를 유발하며, 회전축이나 날개 회전율에 변조되어 추진기 관련 정보를 원거리 전송하는 현상이 발생한다. 이로 인하여 정숙성이 요구되는 선박에서는 추진기 공동소음에 대한 이해와 감소기술 연구가 중요시 되고 있다.^[4]

추진기의 공동현상 예측은 유동장, 와류특성 및 공동핵 등을 고려한 수치해석에 기초한 추정방법과 추진기 모형시험을 통한 음향학적, 시각적 판단 방법이 있다. 수치해석은 정확한 유동장 모사, 날개 끝 와류의 재구성과 기포동역학 모델을 바탕으로 Blade-Tip Vortex Cavitation(BTVC)^{[5], [6]}를 추정하여 공동 초생 속도(Cavitation inception speed, CIS)를 예측하는 방법이다. 추진기 모형시험에 의한 CIS 추정은 일반적인 방법이기는 하나 실선 CIS와는 차이가 있는 것으로 알려져 있다. 이는 레이놀즈 수나 수질 차이 등의 스케일 효과,^[7] 시각적 판단과 음향적 판단의 차이가 원일일 수 있으며, 이와 관련한 연구가 최근 국내외에서 매우 활발히 진행되고 있다. 더불어 CIS를 높이기 위해서는 추진기 설계 단계에서부터 수치적 해석과 모형시험, 실선 결과의 환류 적용이 필요하다.

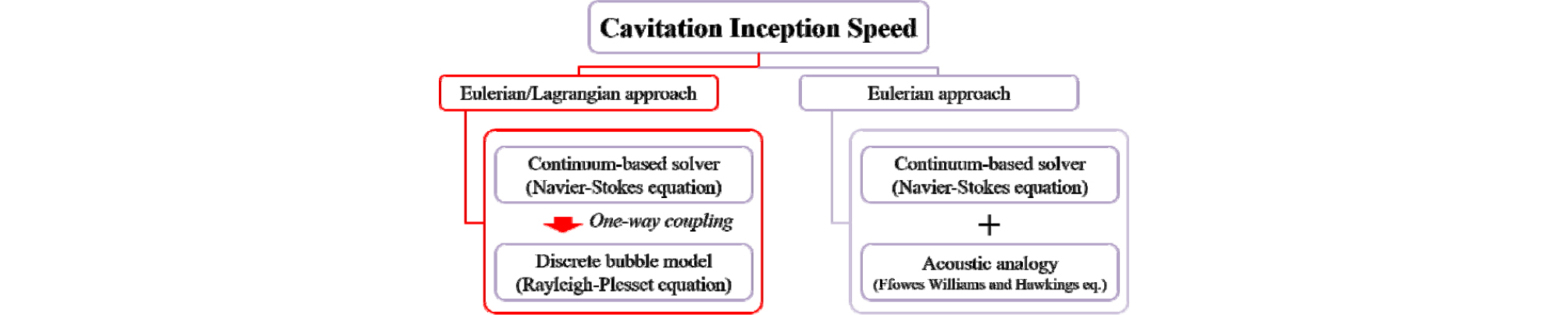
추진기에서 발생하는 유동소음을 예측하기 위한 방안은 Fig. 1과 같이 크게 Eulerian 접근법을 이용한 방안과 Eulerian 접근법에 Lagrangian 접근법을 접목하는 방안으로 구분해서 볼 수 있다. Eulerian 접근법은 일반적으로 공학 분야에서 많이 활용되고 있는 Reynolds-averaged Navier-Stokes(RANS) 혹은 Large- Eddy Simulation(LES)와 같이 물체를 감싸는 가상의 공간을 설정하여 격자계를 형성하고, 경계조건과 시간 변화에 따라 격자계로 설정된 영역 내의 유동변화를 모사하는 방법이며,^{[8], [9], [10], [11]} 소음 해석 시 유동장 내의 물체 표면 혹은, 투과성 적분면을 소음원으로 설정하거나 공동 체적변화 정보를 기반으로 Ffowcs Williams and Hawkings 방정식을 활용하는 Lighthill의 음향상사법에 기반한 소음 해석 방안이 있다.^{[12], [13], [14], [15]}

Fig. 1.

(Color available online) Schematic diagram of cavitation and cavitation noise prediction.

Lagrangian 접근법은 Eulerian 접근법을 통해 얻은 유동장에 공동으로 성장할 수 있는 핵인 공동핵(nuclei)을 다수 분포시켜 공동핵을 하나하나 추적하면서 관측하며, 공동핵의 주변 압력이 충분히 낮아져 기포로 성장할 경우 공동이 발생했다고 판단하는 방법이다. Lagrangian 접근법은 시간에 따른 기포의 크기 변화 정보를 직접적으로 얻을 수 있으며, 크기 변화로부터 기포에 의한 소음을 예측할 수 있다. 따라서 공동의 초생속도를 판단하기 위한 정량적인 기준을 정립할 수 있다는 이점이 있으며, 미국의 DynaFlow에서는 해당 방안을 활용하여 공동 발생을 모사하고 있다.^[16]

따라서 본 연구에서는 앞서 언급한 Eulerian 접근법과 Lagrangian 접근법을 연성하여 NACA16-020 익형의 날개에서 발생하는 BTVC와 이로 인한 공동 소음을 예측하기 위한 연구를 수행하였다. RANS 해석을 기반으로 와류 모델링을 수행하였으며, 와류가 재생된 유동장에 공동핵을 분포시켰다. 공동핵을 대상으로 Rayleigh-Plesset 방정식 기반의 기포동역학 해석을 수행함으로써 기포의 시간에 따른 반경 변화를 모사하였으며, 기포 반경 변화 정보로부터 공동에 의해 수중에 방사되는 소음을 홀극자 소음원으로 모델링하여 예측하였다.

II. 공동현상 수치해석 방법

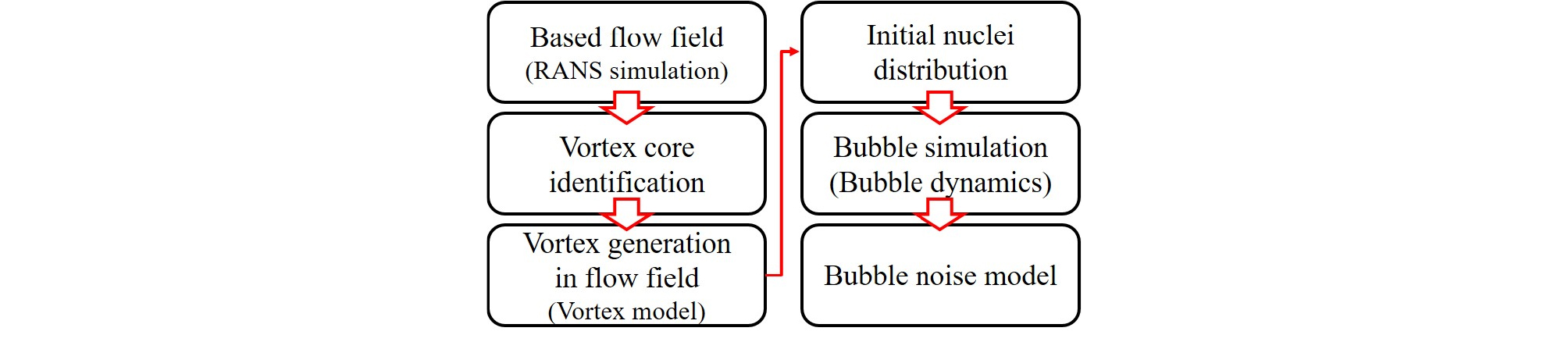
본 연구에서는 Eulerian 접근법에 해당하는 RANS 해석과 Lagrangian 접근법에 해당하는 Rayleigh-Plesset 방정식 기반의 기포동역학을 연성하여 공동해석을 수행하였으며, 전체적인 해석 절차는 Fig. 2에 나타낸 바와 같다.

Fig. 2.

(Color available online) Simulation procedure of Eulerian-Lagrangian one-way coupling method.

먼저 3차원 NACA16-020 익형의 날개를 대상으로 비압축성 RANS 해석을 수행하여 공동핵을 분포시킬 배경 유동장을 구현한다. RANS 해석 결과로부터 얻어진 유동장에 와류 모델을 통하여 소산된 와류 구조를 재생하며, 와류가 재생된 유동장에 공동핵를 분포시킨다. 공동핵의 거동은 주변 유동장 정보로부터 결정되며, 기포동역학 모델을 통해 공동핵의 반경과 위치 변화를 모사한다. 시간에 따른 공동핵의 반경과 위치 정보로부터 공동 기포에 의해 수중에 방사되는 소음을 예측한다.

RANS 해석으로 다상유동을 모사하기 위하여 균일혼상류 모델을 많이 활용하지만 본 연구에서는 유동장 내 공동 현상을 공동핵을 통해 모사하므로 단상유동 해석을 수행하였다. 유동해석은 유한체적법 기반의 상용코드인 Fluent v19.2를 통해 수행하였으며, 일반적으로 3차원 날개에서는 동일한 레이놀즈 수에 대해 유동의 입사각 변화, 그리고 공동 발생 여부와는 무관하게 일정한 궤적의 와류 구조가 형성된다고 알려져 있으므로,^[5] 3차원 정상상태 유동해석을 수행하였다. 유체의 속도와 압력을 연성하는 Semi- Implicit Method for Pressure-Linked Equation(SIMPLE) 방법과 와류 구조를 정확하게 모사할 수 있는 Reynolds Stress Model(RSM)을 통해 비압축성 조건에서도 공동을 잘 예측할 수 있으므로,^[5] 본 연구에서는 비압축성 조건을 채택하였다. 시간과 공간에 대해서는 2차 정확도의 수치 이산화 기법을 적용하였으며, 3차원 정상상태 비압축성 지배방정식은 Eq. (1)과 같다.

비압축성 가정에 의해 유체의 밀도($\rho$)는 상수이며, 유체의 연속방정식과 운동량방정식은 유체의 속도 벡터($\overrightarrow{v}$)와 압력($p$), 유동의 점성($\mu$)과 단위 텐서($I$)를 포함하는 응력텐서($\overline{\overline{\tau }}$)로 표현된다.

RANS 해석은 와류 구조 내에 조밀한 격자를 유지하지 못할 경우 수치적 감쇄로 인해 와류 강도가 소산되는 문제가 있다. 그러나 조밀한 격자를 채택할 경우 해석 비용이 지나치게 크므로, 본 연구에서는 와류 모델링을 통해 와류 강도를 유지하고자 하였다. 이를 위한 선행 조건으로 와류 모델링의 중심축이 되는 와류핵을 특정해야만 한다. 와류핵을 특정하기 위한 방안으로 본 연구에서는 유동속도 구배($\nabla \overrightarrow{u}$)의 대칭 성분인 변형률 텐서와 비대칭 성분인 와도 텐서의 제곱합의 두 번째로 큰 고유치인 λ₂- Criterion을 채택하였으며, 대부분의 유동장에서 범용적으로 와류 구조를 잘 찾아낼 수 있다는 이점이 있다.^[17] 유동의 3차원 날개에서 와류 구조는 유동 방향에 수직한 단면에 대해 형성되므로, 2차원 단면에 대해 최소의 λ₂를 가지는 지점을 와류핵의 위치로 정의할 수 있다. 유동 방향을 x방향이라고 할 경우 2차원 y-z 단면에 대한 유동속도구배는 y방향 속도($v$)와 z방향 속도($w$)에 의해 정의되며, λ₂는 Eq. (2)와 같다.

와류 모델은 와류핵 내부는 강체 회전, 외부는 퍼텐셜 와류로 가정하며, 본 연구에서는 Eq. (3)과 같이 Scully vortex model을 활용하였다.

와류핵을 중심으로 하는 회전방향 속도($V_{\theta }$)와 압력(P)은 와류핵의 반경($a_c$)과 순환($\Gamma$), 와류핵의 중심으로부터의 거리($r$)에 대한 함수로 표현된다.

공동 발생 정도는 공동 수(cavitation number) 외에도 수질에 따라 상이하며, 수질은 물 속의 공동핵의 개수, 크기로 정의할 수 있다.^[18] 본 연구에서 고려한 공동핵 분포는 Table 1과 같다.

Table 1. Number of initial nuclei.

유동장 내에 분포된 공동핵의 상태량은 주변 유동장 정보를 기반으로 정의된다. 공동핵의 반경 및 위치 변화는 기포를 완전한 구형으로 가정하는 Rayleigh- Plesset 방정식과 운동방정식인 기포 궤적 방정식으로 모사하였다. 관련 방정식은 각각 Eqs. (4), (5)와 같다.

기포의 반경($R$)을 모사하는 Rayleigh-Plesset 방정식은 기포 반경의 시간에 대한 1차 미분항($\dot{R}$)과 2차 미분항($\ddot{R}$)을 포함하며, 유체의 증기압($p_v$), 초기 기포 반경($R_0$)과 초기 기포 내 가스 압력($p_{g_0}$)에 의한 국부적인 내부 압력 변화, 외부 유체의 압력($p$), 기포 표면 장력($\gamma$) 및 외부 유체의 점성($\mu$)에 의한 감쇠, 외부 유체와 기포 간의 속도 차이($\overrightarrow{U}-{\overrightarrow{U}}_b$)에 기인한 운동에너지를 고려하여 반경 변화를 모사한다.

Eq. (5)의 우측항은 순서대로 중력($g$)에 의해 기포에 작용하는 부력, 기포 체적($V_b$)에 비례하는 압력 구배, 기포의 투영면적($A_b$)에 작용하는 항력($C_D$), 부가질량 효과 그리고 현재 시간($t$) 및 지연 시간($\tau$)을 고려한 Basset 항이며, 마지막 항은 다른 항들에 비해 효과가 미미하므로 무시한다. 하첨자 $b$는 기포의 물리량이며, 하첨자가 없는 항들은 주변 유체의 물리량이다.

고전적인 Rayleigh-Plesset 방정식은 Eq. (4)의 가장 마지막 항인 주변 유체와 실제 기포의 속도 차를 반영하지 못하였으며, 기포의 표면 정보는 기포가 없다고 가정했을 때의 기포 중앙에서의 유동장 정보와 동일하다고 가정함으로써 기포 크기 변화에 따른 표면 정보를 제대로 정의하지 못해 기포가 과도하게 커지는 문제가 있다. Hsiao et al.^[16]은 이러한 문제를 해결하기 위해 기포 표면의 정보를 위치별로 산출하여 평균하는 Surface Averaged Pressure(SAP) 방법을 제안하였다. 본 연구에서도 동일한 방안을 채택하여 액체에 의한 물리량인 $p$와 $\overrightarrow{U}$에 대해 기포 표면에서의 평균값을 이용함으로써 개선된 형태의 Rayleigh- Plesset 방정식을 적용하였다.

공동핵은 주변의 압력이 공동핵이 성장할만큼 충분히 낮아질 경우 폭발적으로 성장하여 공동 기포를 형성하며, 이 때의 압력을 임계압력($p_{cr}$)이라 한다.^[19]

공동핵은 $\mu m$ 단위의 매우 작은 크기이므로 분자간의 인력이 강하게 작용하기 때문에 공동핵의 크기가 작을수록 더 낮은 임계압력을 지닌다.^[20]

본 연구에서는 공동의 형태를 완전한 구형으로 가정하고 있으므로, 공동 기포에 의한 소음은 홀극 소음원으로 가정할 수 있으며, 이러한 가정으로부터 공동 기포에 의한 소음을 Eq. (7)과 같이 예측할 수 있다.^[21]

기포에 의해 수중으로 방사되는 음압($p_a$)은 지연시간($t\text{'}$)과 관찰자시간($t$), 수중에서 음파의 전파속도($c$), 기포 중심에서 수음점까지의 거리($l$) 및 기포 반경에 의해 정의된다.

III. 해석 결과

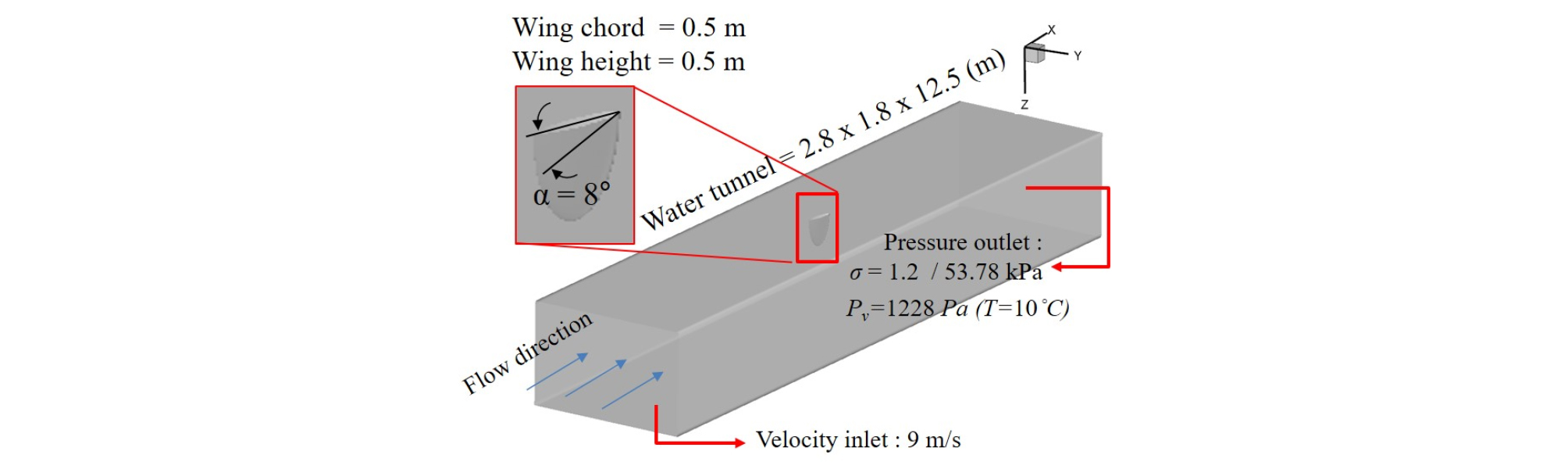
Fig. 3은 RANS 해석에 사용된 해석 영역과 경계조건을 나타내며, 선박해양플랜트연구소(Korea Research Institute of Ships & Ocean Engineering, KRISO) 저소음 대형 캐비테이션 터널(Low Noise Large Cavitation Tunnel, LCT)^[22]의 시험수조 크기와 동일하다. NACA16-020의 받음각은 8°, 입구는 속도 조건, 출구는 압력 조건을 주었으며, 유속은 9 m/s, 출구 압력은 53.78 kPa이다. 유체의 온도를 10 °C이므로 증기압은 1,228 Pa이다. 이러한 조건은 비교대상인 실험조건에 따라 결정하였다.

Fig. 3.

(Color available online) Computational domain and boundary condition.

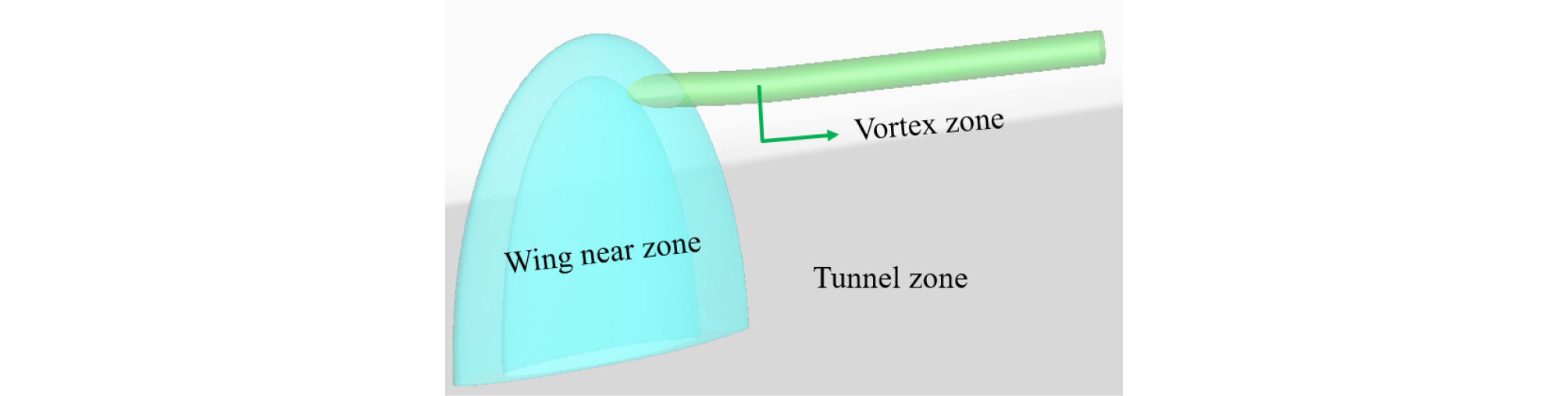
Fig. 4는 해석 격자 영역으로, 각각 날개를 포함하는 영역, 와류 영역, 전체 터널 영역으로 구분할 수 있으며, 격자 수는 날개 영역에 14.6 M, 와류 영역에 3 M, 터널 영역에 4.5 M를 적용하였다.

Fig. 4.

(Color available online) Grid region.

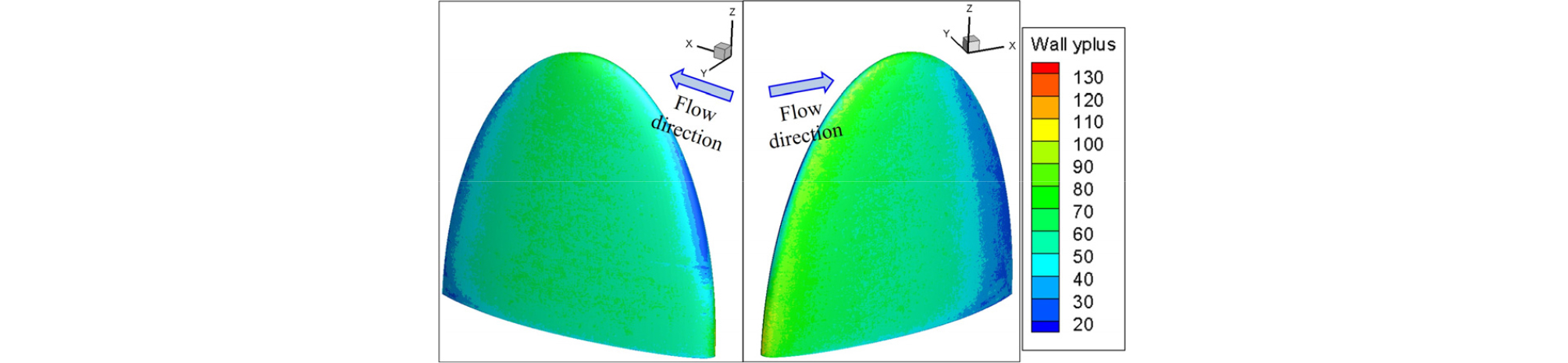
벽면에서 발달하는 경계층 분포를 잘 예측하기 위하여 Fig. 5에 날개 표면에서의 첫 번째 격자높이에 대한 무차원 수인 y⁺ 분포를 나타내었다. y⁺는 벽면에서 첫 번째 격자까지의 거리를 의미하는 무차원 수이며 Eq. (8)과 같이 벽면 근처에서의 마찰속도($u_{fric}$)와 벽면에서 첫 번째 격자까지의 거리($y$) 그리고 국부 위치에서의 유체의 운동학적 점성계수($\nu$)에 의해 정의된다.

Fig. 5.

(Color available online) Wing surface y⁺ distribution.

앞전과 뒷전에서는 $y^{+}\approx$20 ~ 30 정도의 낮은 값을 지니며, 그 외의 표면에서는 100 미만의 값을 가지는 것을 확인할 수 있다. Park^[23]은 선체 주위 유동을 대상으로 50 < y⁺ < 150의 범위에서 선체주위 파형과 저항계수를 추정하였으며, 실험과의 비교를 통해 잘 일치하는 결과를 제시한 바 있다. Fig. 5로부터 본 연구에서의 y⁺는 해당 범위에 속하는 것을 확인할 수 있다.

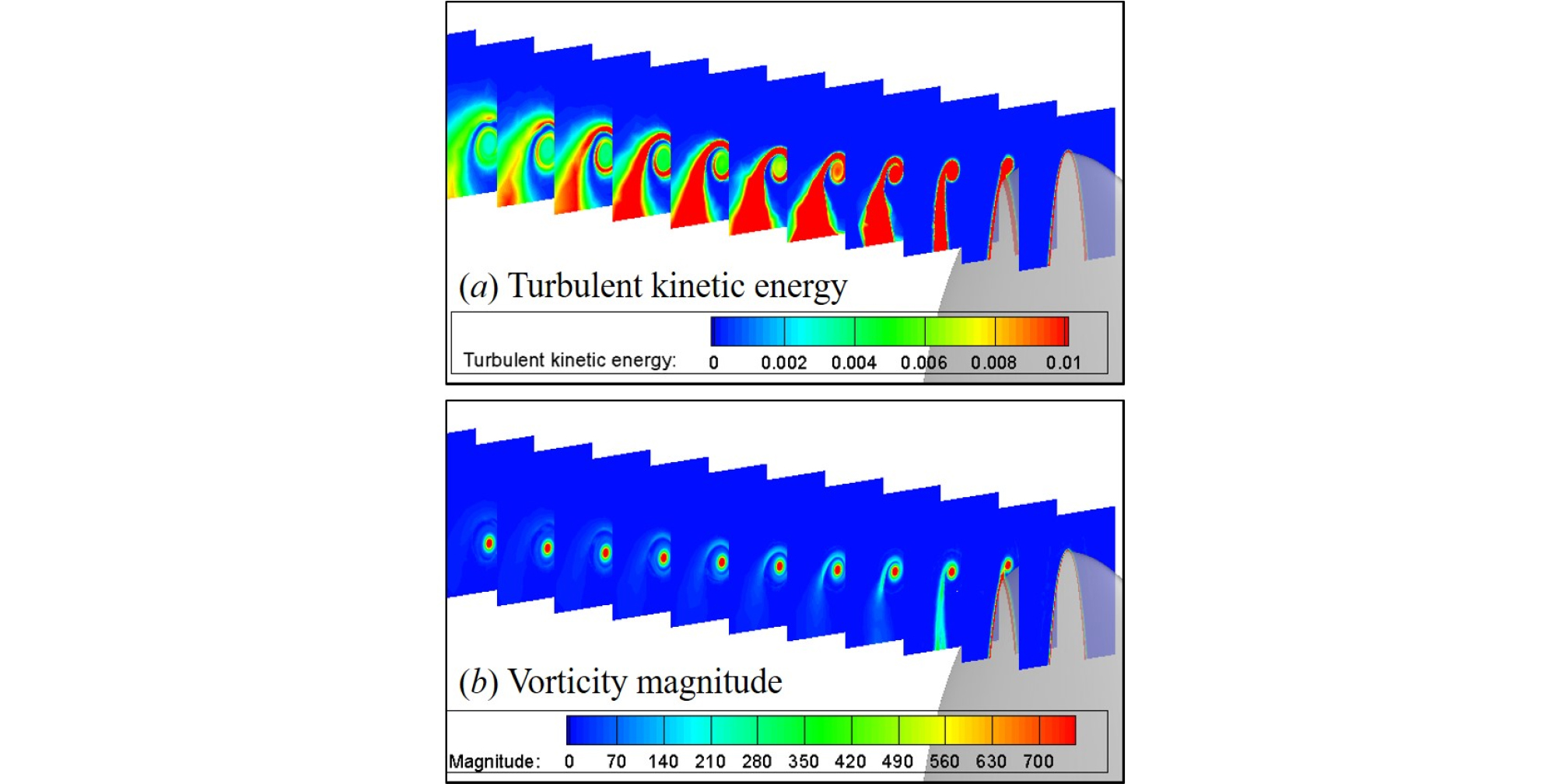
Fig. 6은 RANS 해석 결과를 나타내며, 날개 하류 방향으로의 난류 운동 에너지와 와류 크기를 나타낸다. 난류 운동 에너지로부터 와류 구조가 하류 방향으로 갈수록 소산되는 것을 확인할 수 있으나 전체적으로 와류 구조가 잘 형성되고 있는 것을 확인할 수 있다. 하지만 하류방향으로 갈수록 점차 확산되는 것을 확인할 수 있다.

Fig. 6.

(Color available online) Simulation results; (a) turbulent kinetic energy, (b) vorticity magnitude.

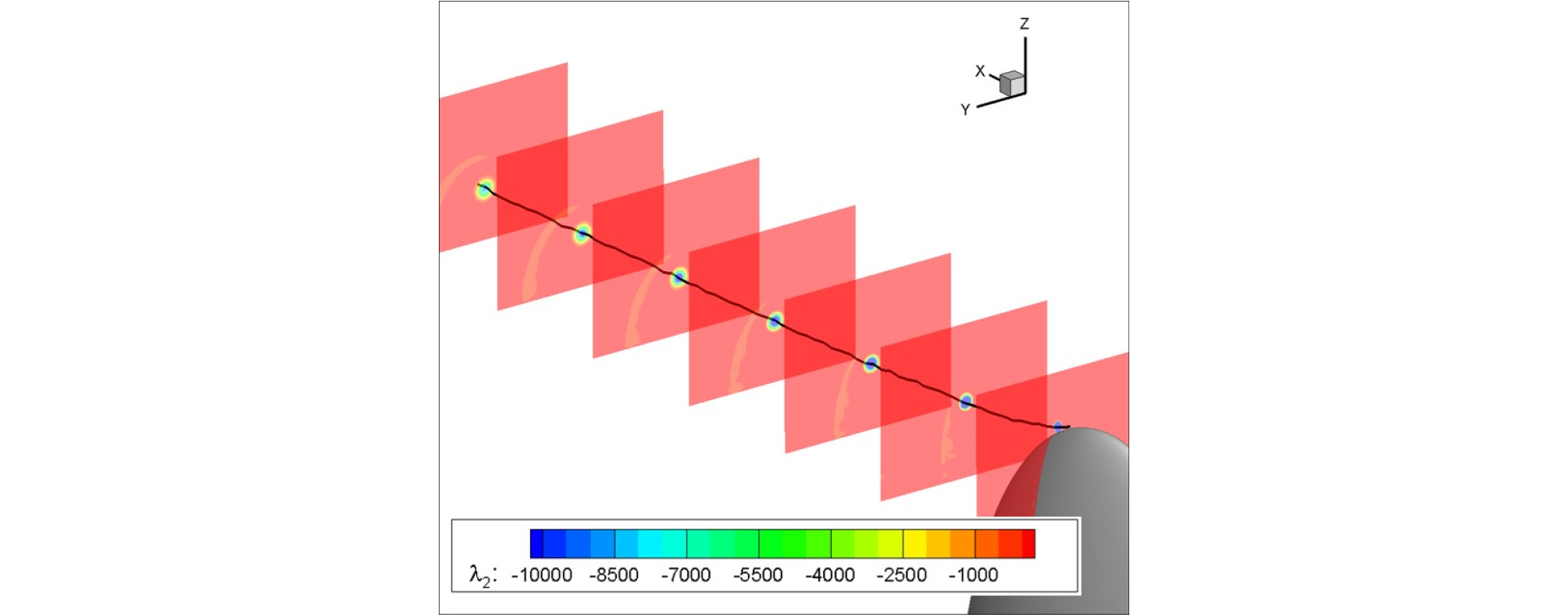
Fig. 7은 하류 방향을 따라 최소 λ₂를 나타낸 그림이며, 이를 통해 와류핵의 위치를 특정할 수 있다. λ₂를 이용한 와류핵의 위치 추정은 와류가 하류방향으로 갈수록 확산되어도 비교적 정밀하게 예측함을 알 수 있다.

Fig. 7.

(Color available online) Minimum λ₂ and vortex core line.

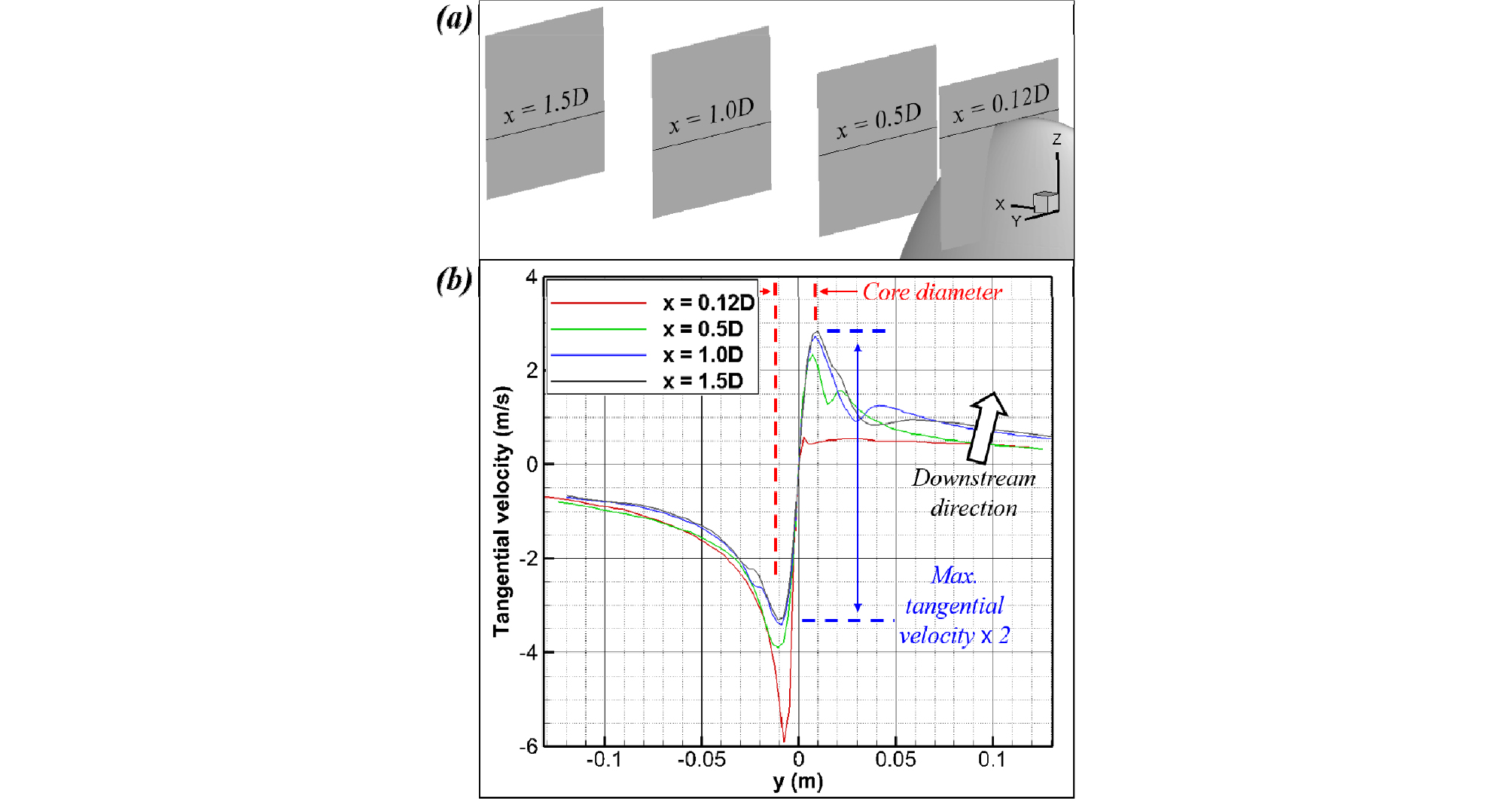
Fig. 8은 날개 끝으로부터 0.12D, 0.5D, 1.0D, 1.5D만큼 떨어진 지점에서의 접선속도 분포를 나타낸 그림이며, 1D는 날개의 시위길이를 의미한다. 속도 분포의 변화를 원활하게 비교하기 위하여 접선속도가 0 m/s인 지점이 y = 0 m에 오도록 각 위치에서의 속도 분포를 겹쳐서 나타내었다. 날개 끝에서부터 강한 회전 성분의 속도가 유도되어 하류 방향을 따라 와류 구조를 형성해가는 것을 확인할 수 있으며, 와류 구조가 형성됨에 따라 속도 분포에서 최대, 최소의 속도를 가지는 지점 간의 거리가 와류핵의 직경, 그 절반을 와류핵의 반경으로 정의할 수 있다. 또한 접선 속도의 최대, 최소 속도 차이의 반을 초기 와류가 지니는 최대 접선속도로써 정의하였다.

Fig. 8.

(Color available online) (a) Extraction regions of tangental velocity profile at x = 0.12D, 0.5D, 1.0D, 1.5D; (b) vortex core radius and maximum tangential velocity from tangential velocity profile.

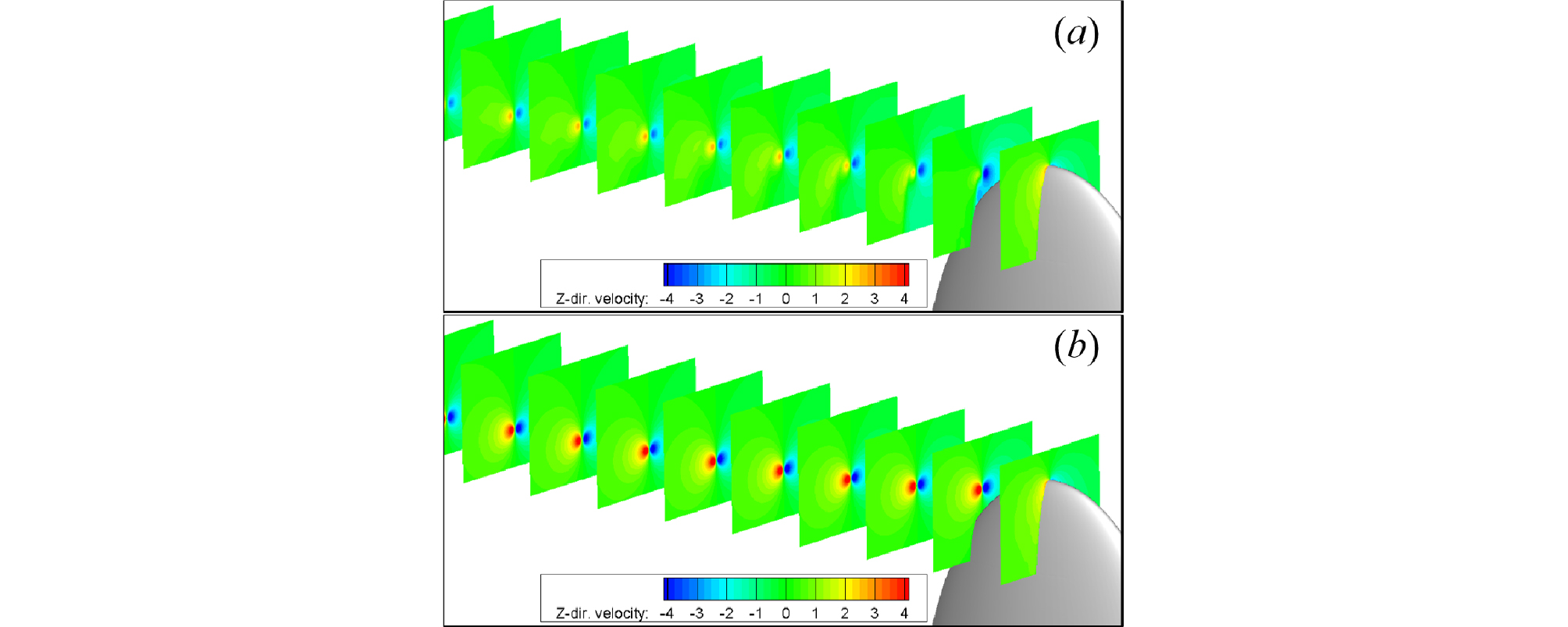
Fig. 9는 유동해석 결과와 유동해석결과를 기반으로 와류 모델링을 수행한 결과이며, Z방향 속도이지만 입구 유속에 수직한 평면에서의 속도이므로 반경방향 속도를 의미한다. Fig. 9(a)가 와류 모델링 수행 전의 유동해석 결과이며, Fig. 9(b)는 와류 모델링을 수행한 후의 유동장 결과이다. 이를 통해 와류의 강도가 하류 방향을 따라 잘 유지되는 것을 확인할 수 있다.

Fig. 9.

(Color available online) Z-direction velocity contours; (a) original RANS flow field; (b) vortex modelled flow field.

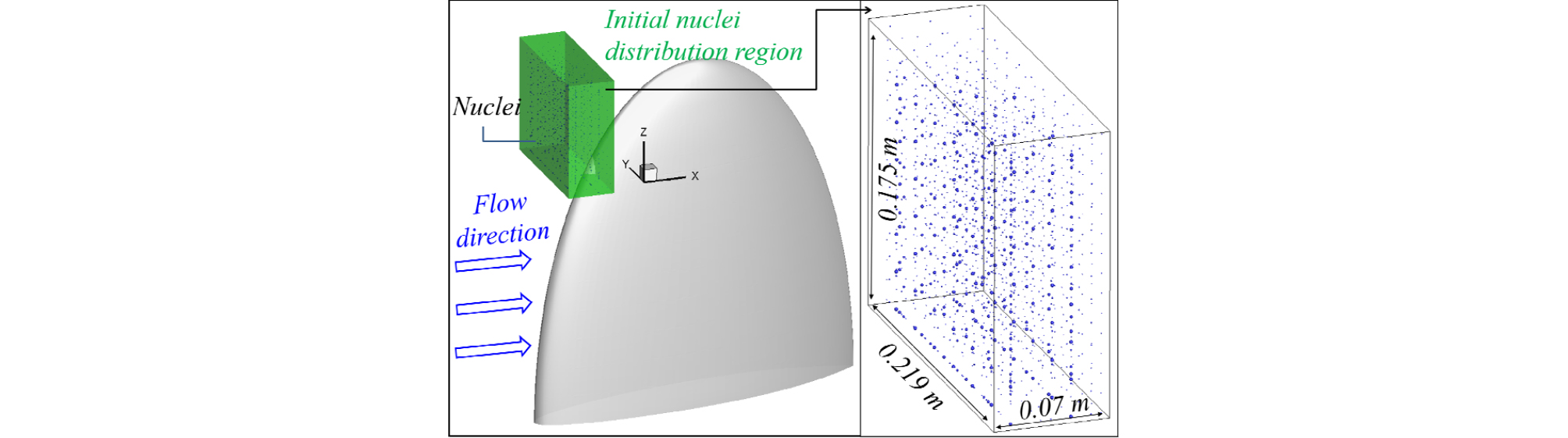
Fig. 10은 초기조건으로 날개 주변의 공동핵 분포 위치를 나타낸 그림이며, 내부의 공동분포를 함께 나타내었다. 공동분포는 수중에 균질하게 분포하고 있다고 가정하였으며, O’ Hern et al.^[18]의 결과로부터 Table 1에 나타낸 8가지 초기 공동핵 크기에 대한 개수만큼 분포시켰다.

Fig. 10.

(Color available online) Initial nuclei distribution region.

공동핵의 상태량은 와류가 재생된 RANS 유동장 정보를 기반으로 형상함수를 도입하여 공동핵 표면으로의 보간을 통해 정의하였으며, 형상 함수는 Eqs. (9), (10)과 같다.

여기서

형상 함수에서 일반화 좌표계의 각 방향에 해당하는 ξ, η, ζ의 정보를 정의하기 위하여 반복 계산법인 Newton-Raphson 방법을 적용하였다.^[24]

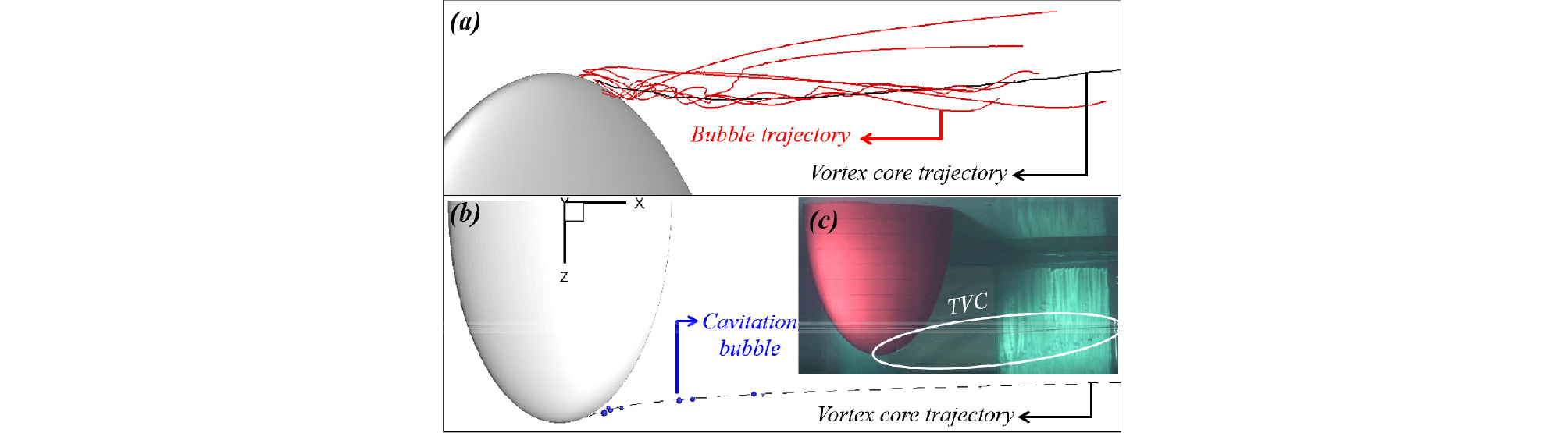
Fig. 11(a)는 유동장 내 성장한 기포에 대해 기포동역학 해석 결과를 기포의 이동 궤적으로 나타낸 그림이다. 이를 통해 와류핵 근처의 공동핵은 와류핵의 저압부로 인하여 공동 기포로 성장하며, 와류핵의 궤적을 따라 나선형의 운동을 보이는 것을 확인할 수 있다. Fig. 11(b)와 (c)에서 유동장 내에서 성장한 기포 형상을 실험결과와 비교하였다. 날개 끝 와류 중심을 따라 공동 발생을 실험결과와 유사하게 예측함을 확인할 수 있다. 하지만, 실험영상의 경우 공동이 실처럼 형성이 되지만 수치결과의 경우 구형의 공동이 날개 끝 와류 중심을 따라 산발적으로 형성됨을 확인할 수 있다. 이는 구형으로 가정한 기포 동역학 모델에 한계에 기인하는 것으로 판단된다. 성장한 기포는 와류핵에서 멀어질수록 다시 소멸하며, 와류핵에서 멀리 떨어진 공동핵은 주변 유동을 따라 흘러가는 것을 확인할 수 있다.

Fig. 11.

(Color available online) Bubble simulation results; (a) bubble trajectory; (b) bubble flow field; (c) BTVC observation in LCT.

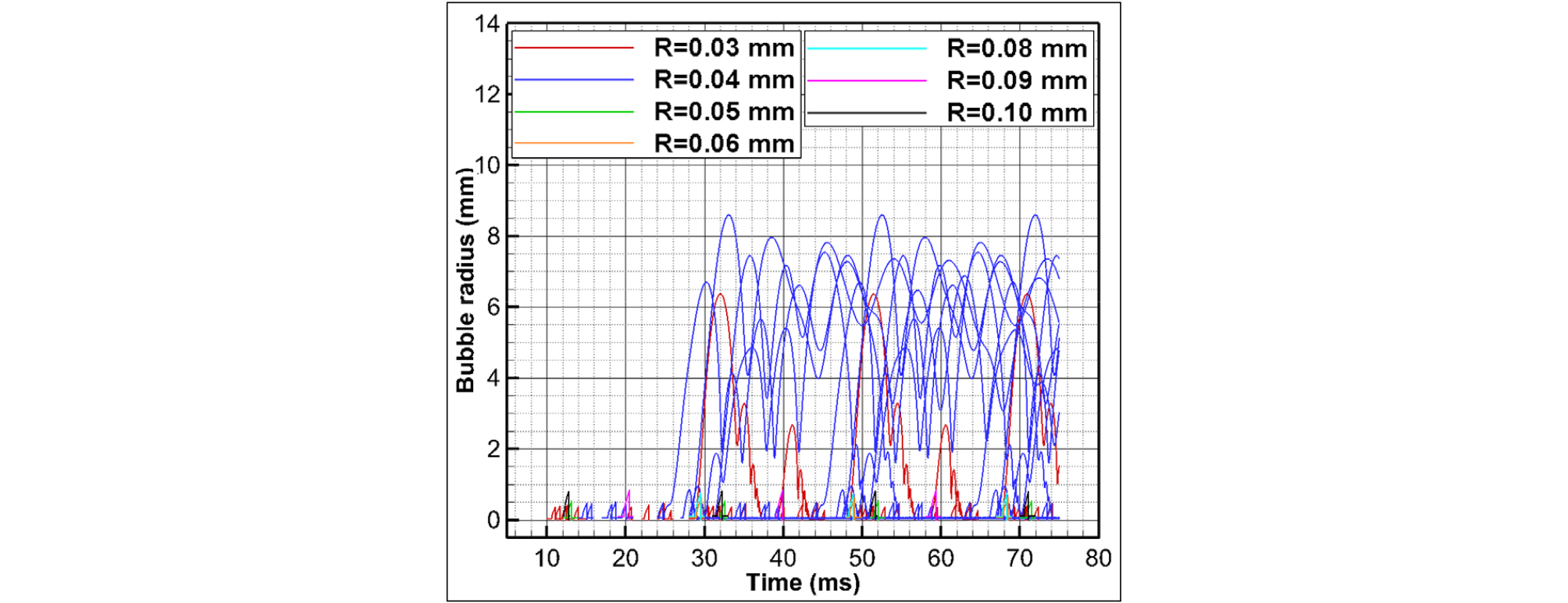
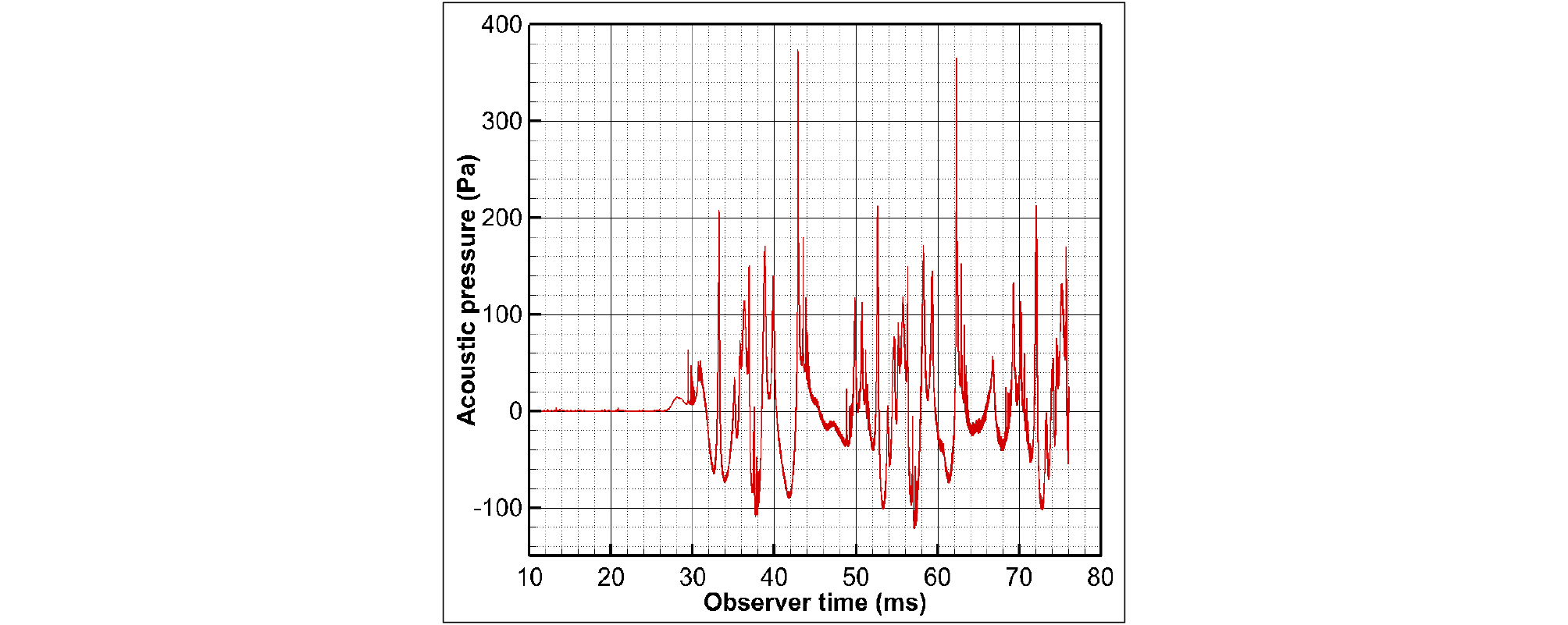
Fig. 12는 시간에 따른 공동핵의 반경 변화를 나타내고 있으며, Fig. 13은 공동핵 각각을 홀극음원으로 모델링하여 예측한 시변 음압을 나타낸 그림이다. 수음점은 날개 끝으로부터 수직 방향으로 1 m 떨어진 지점이다. 유동장 내 분포한 공동핵의 개수가 가장 많은 30 $\mu m$와 40 $\mu m$가 공동 기포로 크게 성장하였으며, 그 외의 다른 크기의 공동핵들도 성장하였으나 비교적 작게 성장한 것을 확인할 수 있다.

Fig. 12.

(Color available online) Bubble radius variation.

Fig. 13.

(Color available online) Bubble acoustic pressure.

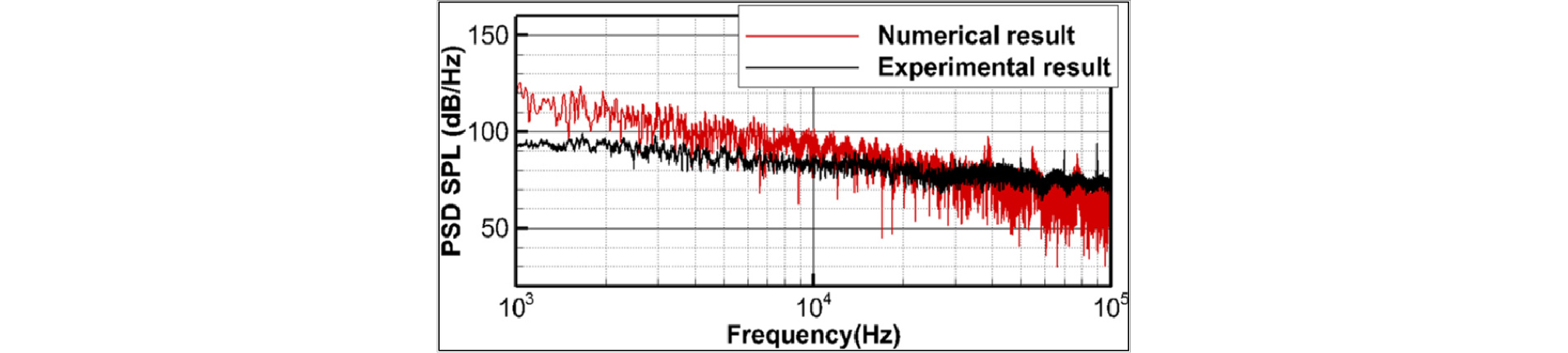
홀극원은 부피의 시간 변화율의 변화율 즉 가속도에 비례하는 것을 고려할 때, 공동기포에 의한 소음은 공동의 반경 변화가 크게 발생하는 성장할 때와 소멸할 때 발생하는 것으로 알려져 있다. Fig. 14에서 동일한 조건으로 선박해양플랜트연구소에서 진행한 실험을 통하여 측정한 음압스펙트럼을 Fig. 13의 결과로부터 얻은 예측 결과와 비교하였다. 두 결과가 전체적으로 유사한 스펙트럼을 나타내며 특히 고주파수 영역에서 잘 일치함을 확인할 수 있다. 하지만 20 kHz 이하의 영역대에서 저주파수로 갈수록 수치해석결과가 측정값보다 음압레벨을 높게 예측하고 있다. 이는 측정환경이 터널형으로 밀폐되어 있어 파장이 커질수록 오차가 커지는 것이 한 이유로 사료된다. 또한, Fig. 11의 결과에서 알 수 있는 것처럼 수치해석에서는 구형의 기포동역학 모델을 사용하여 캐비테이션을 예측함으로써 와류핵에서 캐비테이션이 점음원 형태로 존재하는 것과 달리 실험결과에서는 와류핵에 포획된 기포핵이 구형으로 팽창하지 않고 하류방향으로 보다 크게 팽창함으로써 공동이 실처럼 형성이 되어 선음원처럼 작용하는 현상도 한 원인으로 생각된다.

Fig. 14.

(Color available online) Comparison of power spectral density SPL between numerical result and experiment result.

IV. 결 론

본 연구에서는 추진기에서 가장 먼저 발생하는 공동 현상인 BTVC를 대상으로 그 현상을 모사하고 이에 따른 유동소음을 예측하기 위하여 Eulerian 접근법과 Lagrangian 접근법 연성 해석 방법론을 정립하였으며, NACA16-020 익형의 날개를 대상으로 해당 방법을 적용하였다. 먼저 3차원 정상상태 비압축성 RANS 단상 해석을 수행하였으며, RANS 해석의 수치적 감쇄에 의한 한계를 해결하기 위하여 와류핵을 정의하고 와류 모델링을 수행하였다. 와류가 재생된 유동장에 공동핵을 분포시켰으며, SAP기법이 적용된 개선된 Rayleigh-Plesset 방정식을 통해 기포동역학 해석을 수행함으로써 유동장 내에서 공동 기포의 거동 변화를 모사하였다. 이를 통해 공동핵의 반경변화를 정량적으로 관측하고, 공동 기포의 시변부피를 입력값으로 음압을 예측하여 실험값과 비교함으로써 제시한 방법의 유효성을 확인하였다.

본 연구에서 제시한 수치방법을 활용하면 공동 기포의 반경 정보와 그에 기반한 음압 정보를 획득할 수 있을 뿐만 아니라, 현재 관련 산업계에서 이슈가 되고 있는 공동의 초생속도를 정량적으로 평가할 수 있는 지표를 개발하는데 큰 도움이 될 수 있을 것으로 판단된다. 특히, 모형시험을 통한 CIS 예측값과 실선 CIS 예측값의 차이의 원인을 레이놀즈 수와 수질 차이 등의 스케일 효과를 고려하여 고찰할 수 있으며 이에 대한 추가 연구를 진행중이다.

한편으로는, 구형 기포 동역학 모델의 한계로 실험영상처럼 실처럼 BTVC 결과를 재현하지 못하고 있다. 향후 연구를 통해 보다 정밀한 BTVC 거동을 예측하기 위하여 압축성 효과를 고려한 3차원 기포동역학 모델을 개발할 예정이다.