I. 서 론

RLS(Recursive-least-squares) 알고리즘은 잘 알려진 적응 알고리즘 중에 하나이다.^[1] 본 알고리즘은 통신, 제어 등 다양한 분야에서 쓰이고 있다.^[2],[3] RLS는 적응 신호처리 분야에서 많이 쓰이는 또 다른 유명한 적응 알고리즘인 LMS(Least-Mean-Square)보다 빠르게 수렴하고, 잔차 오차도 상대적으로 작다는 것이 널리 알려져 있다. 뿐만 아니라 이 같은 우수함이 LMS와는 달리 입력 신호의 자기 상관 행렬의 고유치 분포차이와 무관한 장점도 있다. 이런 장점에도 불구하고, RLS는 다음과 같은 여러 가지 단점도 가지고 있다.^[4]

(i) 계산량이 상대적으로 많다.

(ii) 입력 신호의 자기 상관 행렬의 역함수를 구하는 과정에서 수치적 불안정이 발생한다.

(iii) 망각인자의 값에 따라 시변 환경에 적응하는 능력이 달라진다.

최근에 역행렬이 필요 없으면서 RLS와 유사한 수렴특성을 나타내는 두 개의 서로 다른 연구가 각각 RI(Recursive Inverse) 알고리즘과 IWF(Iterative Wiener Filter) 알고리즘으로 발표되었다. 두 알고리즘들은 RLS와 유사한 수렴 특성을 나타낼 뿐만 아니라 RLS의 단점 중 하나인 역행렬을 계산에서 오는 수치적 불안정을 해소한 바 있다.^[5],[6] RI 알고리즘은 축차적인 방법의 자기 상관 행렬과 상호 상관 벡터 및 망각인자를 이용한 스텝 상수로 Wiener 방정식의 해를 구하였고, IWF 알고리즘은 급경사법과 그에 쓰이는 스텝상수를 오차 에너지를 최소로 하는 가변 상수로 Wiener 방정식의 해를 구하였다. 이렇게 서로 다른 접근을 사용한 결과가 상당히 유사함도 보였다.^[7]

본 논문에서는 앞서의 두 방법과 다른 접근으로 기울기 평균 벡터를 사용한 가변 스텝을 구하는 방법으로 최소 자승 알고리즘을 제안한다. 그리고 제안된 알고리즘이 형태가 기존의 RI나 IWF와 동일한 형태임도 보인다. 또한 발표된 RI나 IWF가 고정 망각 인자를 사용하는 경우인데 반하여, 본 논문에서는 시변 채널 추정을 원활하게 하기 위해서 가급적으로 부가되는 계산 복잡도가 적은 가변 망각인자를 함께 제안한다.

II. 기울기를 사용한 최소 자승 해법

본장에서는 기울기를 사용한 최소 자승 해법을 요약한다. 본 해법은 오차의 제곱 즉 E(e(k)²)를 최소화하는 하는 것이다. 단 오차의 제곱 값의 평균 E(e(k)²)을 사용하는 대신, 오차의 제곱 순시값 e(k)²를 사용한다.^[2],[3]

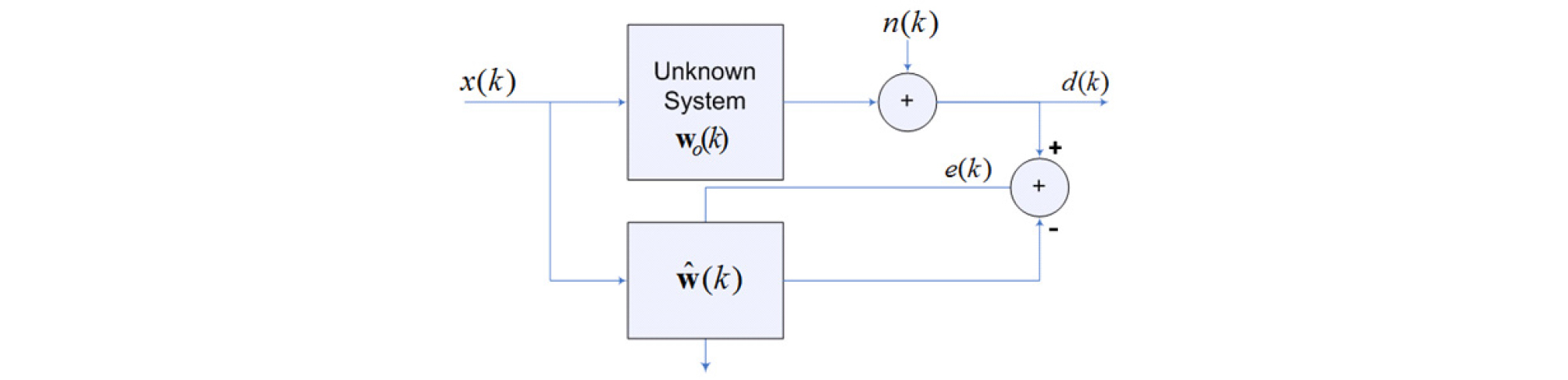
Fig. 1에서와 같이 ${\hat{\mathbf{w}}}^{\mathbf{T}}\left(k\right)=\left[{\hat{w}}_0\left(k\right),{\hat{w}}_1\left(k\right),···,{\hat{w}}_{N-1}\left(k\right)\right]$과 ${\mathbf{w}}_{\mathbf{o}}^{\mathbf{T}}\left(k\right)=\left[w_0\left(k\right),w_1\left(k\right),···,w_{N-1}\left(k\right)\right]$를 각각 추정 시스템 계수 벡터와 참 시스템 계수 벡터라고 하자. 시간 k에서 순시 오차는 다음 식과 같다.

Fig. 1.

A structure of adaptive filtering system.

여기서 $c\left(k\right)=\hat{\mathbf{w}}\left(k\right)-{\mathbf{w}}_0\left(k\right)$이고 H는 허밋 전치(Hermitian Transpose)행렬이다. 순시 오차 e(k)의 제곱 한 후 $\hat{\mathbf{w}}\left(k\right)$에 대한 미분을 적용하면 다음과 같은 식을 얻을 수 있다.

위 순시 미분 값을 사용하여 다음과 같은 추정 시스템 계수 갱신 식이 유도된다.

여기서 µ는 스텝 크기다.

III. 평균 기울기 벡터를 사용한 가변 스텝 크기 최소 자승 알고리즘

가변 스텝 크기를 얻기 위해서 Eq. (4)와 같은 목적함수를 고려한다.

여기서 $e\left(k\right)=d\left(k\right)-{\mathit{w}}^H\mathit{x}\left(k\right)$이다. 그리고 Eq. (4)를 이용한 추정 계수 벡터 갱신 식은 다음 Eq. (5)와 같다.

그리고 목적함수의 미분을 좀 더 자세히 풀면 Eq. (6)과 같음을 알 수 있다.

여기서 행렬 R_n에 대한 갱신식을 다음과 다시 쓸 수 있다.

Eq. (7)에서 보면 행렬 R_n은 새로운 행렬 e(n)x(n)의 지수함수 가중 자기 상관 행렬이라고 할 수 있다. 그리고 벡터 r_n에 대한 갱신식도 다음과 다시 쓸 수 있다.

Eq. (8)에서 보면 벡터 r_n는 행렬 x(n)과 스칼라량 d(n) 사이의 지수함수 가중 상호 상관 벡터임을 알 수 있다. 그리고 Eq. (6)의 목적 함수의 순시 기울기에 대해서 일종의 이동 평균을 취하는 형식을 가진다. 이로부터 순간순간 변동성을 줄이는 효과를 낸다. 그리고 Eq. (6)을 정리하여 다음과 같은 기울기 평균 벡터 갱신식을 얻는다.^[8]

또 가변 스텝 크기는 다음과 목적함수를 스텝 사이즈에 대해서 최소화를 함으로써 다음과 같이 얻을 수 있다.

위 미분 시에 나오는 상수는 무의미하여 생략하고, $W\left(n\right)=W(n-1)+{\mu }_n{g}_{n\overline{)n-1}}$과 $e\left(k\right)=d\left(k\right)-{\mathbf{w}}^H\left(n\right)\mathbf{x}\left(k\right)$도 함께 고려한다. 그 결과를 자세하게 풀어 쓰면 Eq. (11)과 같다. Eq. (11)의 각 항을 따로 묶어 정리하면 Eq. (12)이 된다. Eq. (13)은 Eq. (12)를 행렬과 벡터를 이용하여 정리한 것이다.

위 Eqs. (10)과 (13)으로부터 다음과 같은 가변 스텝 크기가 유도된다.

위 Eq. (4)부터 Eq. (14)까지를 정리하여 새로운 가변 스텝 크기 최소 자승 알고리즘을 정리하면 다음 Table 1과 같이 요약된다.

Table 1. Summary of the proposed algorithm.

위 Table 1을 Reference [5]와 비교하면 서로 동일한 알고리즘임을 알 수 있다. 즉 Reference [5]에서는 스텝 사이즈를 선형 탐색법을 사용하여 구하였고, 본 논문에서는 스텝 사이즈를 기울기 평균 벡터 갱신식을 이용하여 구하였으나 그 최종적인 결과는 서로 같음을 알 수 있다. 따라서 본 논문에서 얻은 알고리즘의 성능이 IWF와 같고 따라서 RLS와도 같음을 알 수 있다.

IV. 가변 망각인자

앞 절에서 유도한 알고리즘은 일견 가변 스텝 사이즈를 가지고 있어서 가변 채널 추정에 적합할 것이라고 생각할 수 있으나, Table 1을 살펴보면 내부적으로 고정된 망각인자를 사용한다. 고정된 망각인자는 유효 데이터 범위를 고정시키게 된다. 이는 시스템의 시변성에 대한 정보가 충분하고, 또 그 성질이 변하지 않는다면 고정된 망각인자를 적용하는 것이 가능하지만, 시스템 시변성 자체가 수시로 변한다면 망각인자를 알맞게 변경하는 것이 바람직하다. 이를 가변 망각인자라고 한다.^[9],[10] 본 절에서는 행렬 미분을 사용하지 않는 가변 망각인자 방법들 중에서 적용 가능한 두 가지 방법들을 골라 적용한다.

4.1 방법1

첫 번째 방법은 Reference [9]에서 사용된 잔차 오차를 사용하는 간단한 가변 망각 인자 계산법이다.

여기서 $L\left(n\right)=-N{\int }_{}^{}\left(\rho e^2\right(n\left)\right)$이고, NINT[ ]는 [ ]에 가장 가까운 정수를 구하는 함수이다.

본 방법을 사용할 때 실제 추가되는 부동 소수점 곱셈은 2이고 지수 계산 1회가 추가된다.

4.2 방법2

두 번째 방법은 다음 식과 같은 가변 망각인자를 도입한 목적함수를 기초도 유도한다.^[10]

여기서

위 식은 다음과 같이 풀어서 표시할 수 있다.

위 식을 가변 망각 인자를 중심으로 다시 쓰면 다음 식과 같다.

그리고 $n\to \infty$와 같이 충분히 수렴된 후에, $J_n\approx J_{n-1}=\mathrm{const}$이 될 것이므로 위 식은 좀 더 간단히 표현할 수 있고 최종적으로 다음 두 단계로 가변 망각인자를 구할 수 있다.

여기서 𝛼는 임의의 작은 크기의 스텝 사이즈이다.

본 방법을 사용할 때 실제 추가되는 부동 소수점 곱셈은 1이다.

V. 시뮬레이션

본 장에서는 시뮬레이션을 통해서 제안한 알고리즘의 수렴 성능을 알아본다. 이를 위해서 시간에 상관없이 특성이 일정한 시불변 시스템에 대해서 Table 1에 요약된 고정 망각인자를 사용한 알고리즘과 4장에서 제안한 두 가지 가변 스텝 사이즈를 적용한 알고리즘 간의 수렴 성능을 비교한다. 그리고 실험 중간에 채널이 갑자기 바뀌는 시변 시스템 시변 시스템에 대해서 각각 수렴 성능을 비교한다.

5.1 시불변 시스템에서 수렴 성능 비교

제안된 알고리즘의 일반적인 수렴 성능을 보이기 위해서 시불변 시스템 환경 하에서 수렴 실험을 하였다. 실험에 사용된 환경을 구체적으로 기술하면, 입력 신호는 -0.5와 0.5 사이의 균일 분포를 이루는 불규칙 신호를 사용하였다. 또 부가 잡음도 같은 균일 분포 불규칙 잡음 사용하였다. 신호 대 잡음비는 25 dB로 하였다. 이런 신호를 사용하여 시스템의 임펄스 응답이 ${\mathbf{W}}_0$= [0.005 0.009 -0.024 0.854 -0.218 0.049 -0.016 -0.016]인 시불변 채널 상에서 일반적인 RLS 알고리즘과 고정 망각인자를 사용한 제안 알고리즘과 가변 망각인자를 사용한 제안 알고리즘 간의 수렴 성능을 각각 비교하였다. 이때 사용한 고정 망각인자 값은 0.99, 0.8로 설정하였다.

Fig. 2(a)에는 망각 인자를 0.99로 고정한 일반 RLS 알고리즘과 고정 망각인자를 사용한 제안 알고리즘 및 가변 망각인자를 사용한 제안 알고리즘을 비교하였다. 그리고 Fig. 2(b)에는 망각 인자를 0.8로 고정한 일반 RLS 알고리즘과 고정 망각인자를 사용한 제안 알고리즘 및 가변 망각인자를 사용한 제안 알고리즘을 비교하였다. Fig. 2(c)와 (d)에는 두 가지 망각인자의 변화를 보였다.

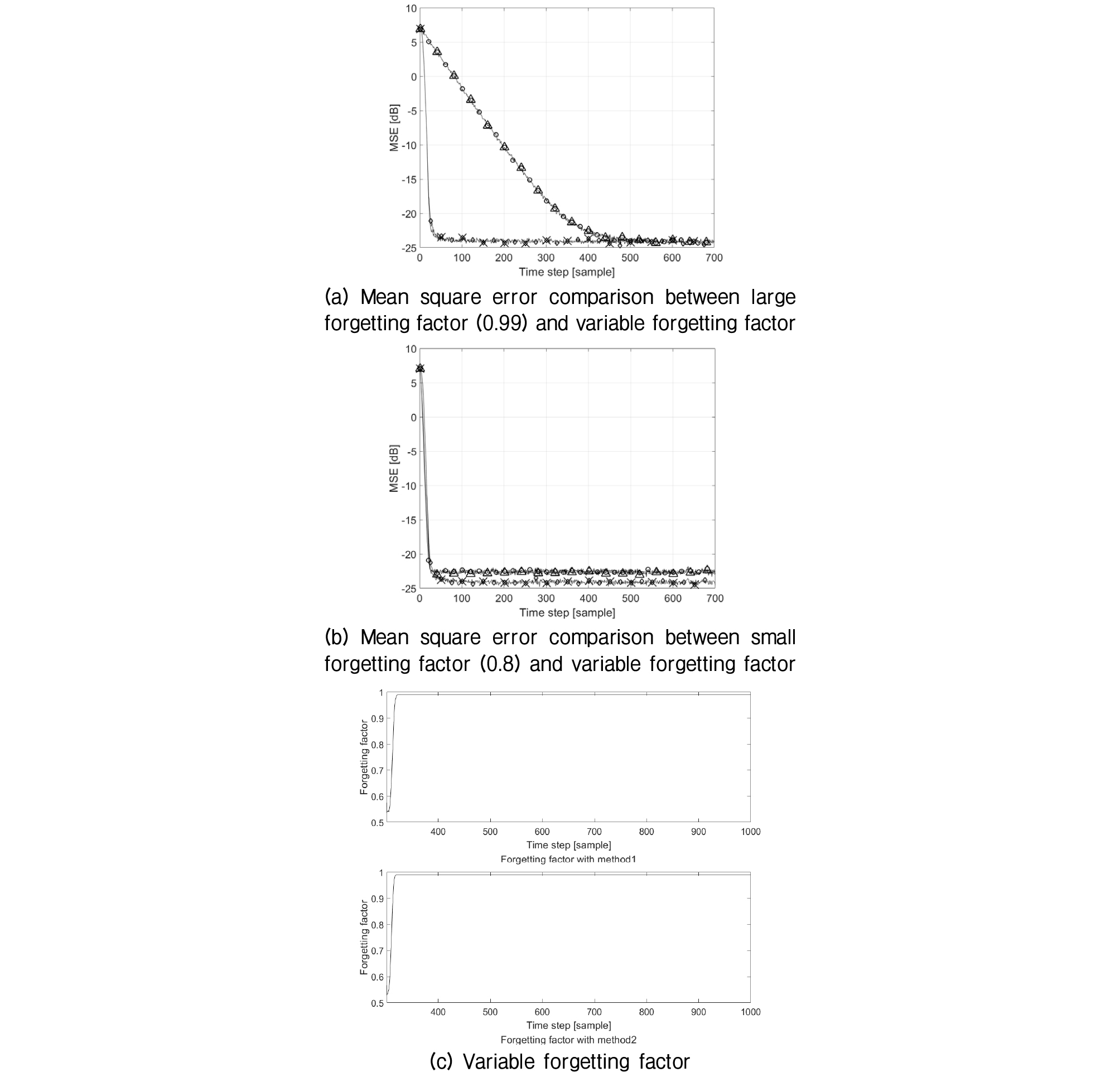
Fig. 2.

Convergence performance comparison in the time invariant channel (a) mean square error comparison (-○-: RLS, -△-: proposed algorithm with fixed forgetting factor, -◇-: proposed algorithm with variable forgetting factor method 1, -×-: proposed algorithm with variable forgetting factor method 2) (b) comparison between two variable forgetting factor methods.

1에 가까운 망각인자를 사용한 Fig. 2(a)에서는 고정 망각인자를 사용하는 알고리즘들은 수렴이 늦고 가변 망각인자를 사용하는 경우는 수렴이 빨랐다. 그러나 최종 수렴 수준은 같았다. 반면에 비교적 짧은 망각인자 값인 0.8을 사용한 Fig. 2(b)에서는 고정 망각인자를 사용한 경우와 가변 망각인자를 사용한 경우가 비슷한 수렴 속도를 보인다. 그러나 최종 수렴 수준은 고정 망각 인자를 사용하는 경우가 상대적으로 큰 MSE (Mean Square Error)를 보였다. 이같은 결과는 Fig. 2(c)를 살펴보면 이유를 알 수 있다. 즉 가변 망각 인자의 경우 망각인자를 점차적으로 1에 가깝게 변화 시켜서 추정 데이터 윈도 길이를 늘이는 효과를 만들어서 추정 오차를 줄이게 되는데 반해서 고정 망각인자의 추정 데이터 윈도 길이를 짧은 상태로 고정하게 되어 수렴 속도는 빠르나 수렴 후 추정 오차가 상대적으로 크게 되는 것이다.

5.2 급격하게 변하는 시변 시스템에서 수렴 성능 비교

제안된 두 알고리즘의 성능을 보기 위한 또 다른 경우로써 급격히 변하는 시변 시스템 환경 하에서 수렴 실험을 하였다.

실험에 사용된 환경을 구체적으로 기술하면, 입력 신호와 부가 잡음은 이전과 같고, 시변 시스템을 모사하기 위해서 처음부터 300번 샘플까지는 시스템의 임펄스 응답이 ${\mathbf{W}}_{01}$= [1, 0.8668, -0.4764, 0.2070]이다가 301번 샘플부터 임펄스 응답이 ${\mathbf{W}}_{02}$= [1, -0.8326, 0.6656, -0.7153]로 갑자기 변하는 시변 채널 상에서 고정한 일반 RLS 알고리즘과 고정 망각인자를 사용한 제안 알고리즘 및 가변 망각인자를 사용한 제안 알고리즘을 비교하였다. 이때 사용한 고정 망각인자 값은 0.98로 설정하였다. 그리고 제안한 두 개의 가변 망각 인자 변화도 함께 도시하였다.

Fig. 3(a)를 보면 제안한 가변 망각인자를 사용하는 두 개의 알고리즘들은 300 샘플 이전에 수렴이 되어 낮은 잔차를 유지하며, 갑자기 새로운 채널로 바뀌는 경우에도 변화된 채널 상황에 맞춰서 신속히 적응하고 있는 것을 알 수 있다. 반면에 고정 망각인자의 경우 채널 변화 후에 상당이 오랫동안 높은 추정 오차를 보였다. 그 이유는 망각인자가 1에 가까운 값으로 고정되어 있어서 긴 추정 윈도우 길이를 유지하여 새로운 채널을 추정하는 과정에도 여전이 이전 채널의 영향을 받고 있기 때문이다. Fig. 3(b)는 두 가지 방법의 가변 망각인자의 변화를 보여주고 있다. 가변 망각인자는 갑자기 변하는 시점에 아주 작은 값을 갖도록 변하였다가 다시 1에 가까운 원래 값을 유지한다. 두 가변 인자의 거동은 유사하다 따라서 실제 구현 시에 복잡도의 차이를 바탕으로 선택을 하면 된다.

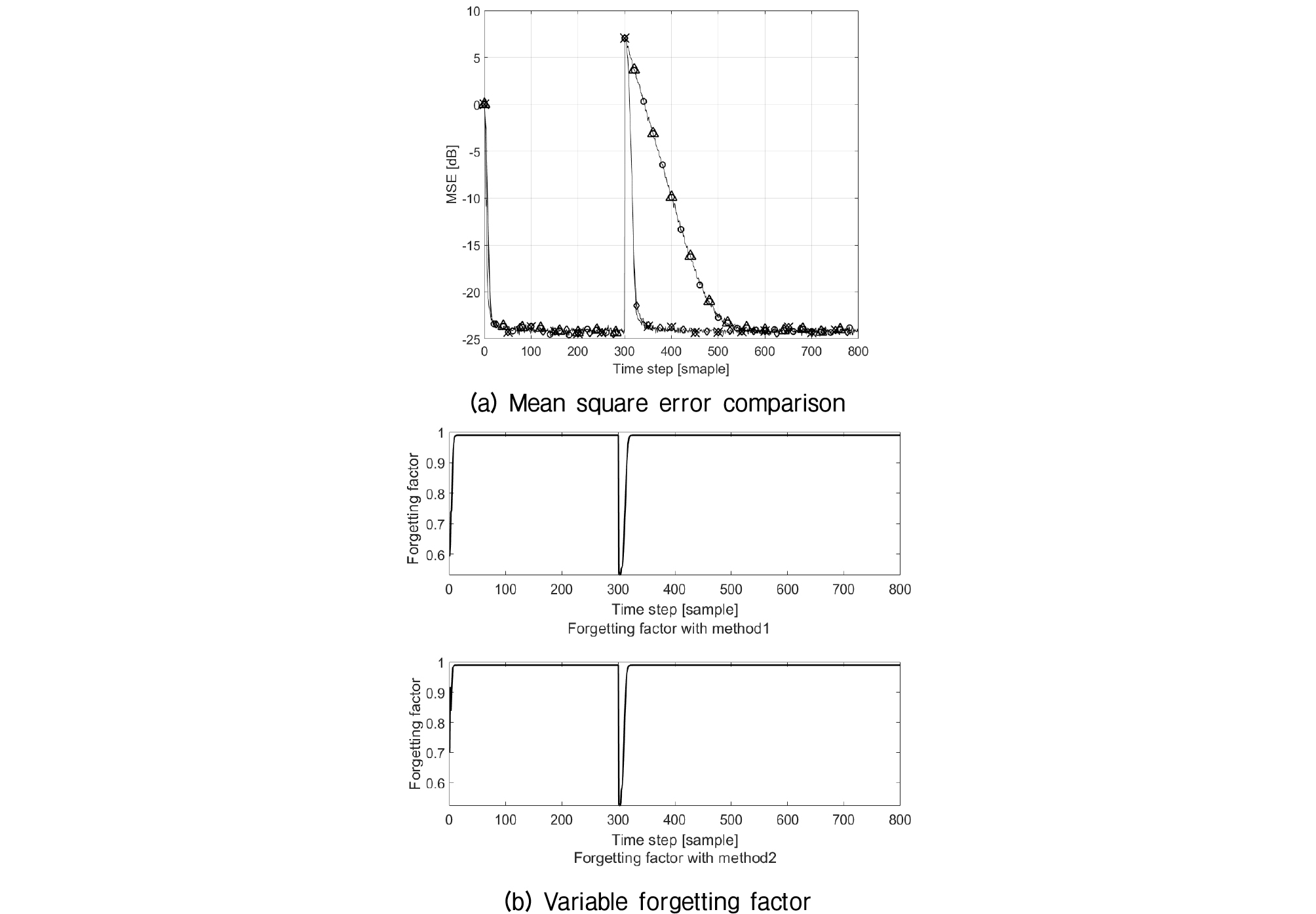
Fig. 3.

Convergence performance comparison in the time invariant channel (a) mean square error comparison (-○-: RLS, -△-: proposed algorithm with fixed forgetting factor, -◇-: proposed algorithm with variable forgetting factor method 1, -×-: proposed algorithm with variable forgetting factor method 2) (b) comparison between two variable forgetting factor methods.

VI. 결 론

본 논문에선 RLS의 불안정성을 초래하는 역행렬을 사용하지 않으면서 대등한 수렴성을 보이는 방법을 기울기 평균 벡터를 사용한 가변 스텝 최소 자승을 사용하여 제안하였다. 제안한 방법은 역행렬을 사용하지 않으면서 고속의 수렴성을 갖는 RI이나 IWF방법과 같은 절차의 알고리즘이 됨도 보였다. 또 시변 채널 추정에 알맞도록 가변 망각인자도 함께 제안하였다. 가변 망각인자로 인하여 추정하는 채널에 따라 알맞은 크기를 망각인자를 제공하여 수렴 속도를 향상시키고 채널 추정 성능도 높이는 효과를 얻었다.