I. 서 론
II. 기존 방법론
2.1 Top-down approach
2.2 Bottom-up approach
III. 제안된 방법론
3.1 문제 정의
3.2 Normalized Spatial Covariance Matrix
3.3 정규화된 공간 공분산 행렬의 적용
IV. 실 험
4.1 실험 조건
4.2 실험 결과
V. 결 론
I. 서 론
칵테일 파티 효과 문제는 실제 환경에서 동시다발적으로 발생된 음원에 의해 혼합된 신호에 대한 전형적인 Blind Source Separation(BBS) 문제와 관련이 있다.[1] BSS는 어떠한 사전 정보 없이 센서로부터 관찰된 신호만으로 혼합된 신호로부터 개별적인 소스를 분리하는 비지도 학습 기법이다.[2] 혼합된 신호로부터 잘 분리된 소스는 향상된 음원 인식 플랫폼을 위한 잡음 환경에서의 목표 음성 추출, 음악 분석을 위해 오케스트라 공연의 각 악기 부분의 분리,[3] 보청기와 같은 청각보조 장치의 성능 향상[1] 등에 활용이 가능하다.
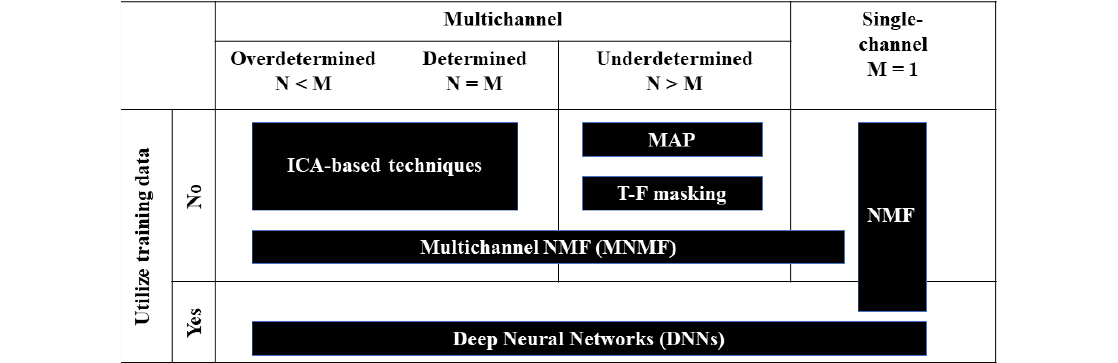
음원 분리 알고리즘은 Fig. 1과 같이 학습데이터의 사용 유무에 따라 두 가지로 나눌 수 있다. 최근에는 컴퓨터의 고속 성능과 Graphics Processing Unit의 보급으로 인해 심층신경망(Deep Neural Networks, DNN)이 많이 연구되고 있다.[4] 즉, 빅데이터 학습을 통해 단일 채널에서 분리를 수행한다. 그러나 이러한 지도학습 알고리즘은 학습하지 않은 데이터에 대해 성능이 저하되는 단점이 있다.[5]
Fig. 1의 사전정보를 활용하지 않는 BSS 영역에서는 마이크로폰과 음원의 개수와 각 방법론들이 가정하는 가설이 다양한 방법론들을 구분 짓는 기준이 된다. 음원을 분리하기에 충분한 마이크 수가 보장되는 경우는 (over-)determined situation으로써 음원의 개수(N)가 마이크의 개수(M)보다 같거나 적은 상황을 의미한다.
이러한 상황에서는 독립 성분 분석(Independent Component Analysis, ICA) 기반의 접근 방식을 활용한 선형 필터는 혼합 신호를 효과적으로 분리할 수 있다. 따라서 1994년도에 처음 제안된 이후로 많은 ICA 기반 기술이 제안되어왔다.[6], [7] 이 방법들은 각 소스가 통계적으로 독립되어 있으며 가우시안 분포가 아닌 것을 가정하여 역혼합 행렬을 추정하는 원리이다. 그러나 실제로 음원 수가 마이크 수보다 많을 수 있으므로 실용성이 떨어진다는 단점이 있다.
마이크의 수가 충분하지 않은 불확실한 상황인 underdetermined situation에서, 희소성 기반 접근법이 사용된다. 즉, 스펙트로그램의 각 시간-주파수 슬롯에 존재하는 소스 하나가 지배적이며 전체 스펙트로그램에서 소스가 존재하는 영역이 적은 상황을 가정하는 접근법이다. 이는 음성 및 음악과 같은 음원이 시간-주파수 표현에서 희미한 특성을 나타내기 때문에 굉장히 유용하며 이러한 특성은 시간-주파수 마스킹 또는 최대 사후 확률 기반 추정알고리즘에 도움이 되는 접근법이다.[8], [9]
본 논문에서는 실용적인 관점에서 Fig. 1처럼 모든 상황에 활용 가능한 Multichannel Nonnegative Matrix Factorization(MNMF)의 성능을 개선하기 위한 연구를 수행하였다. 그 중에서도 Sawada et al.[10]의 MNMF에서 공간 공분산 행렬에 중점을 둔다.
가장 난해한 환경인 underdetermined convolutive 혼합 환경에서, 효과적인 클러스터링을 위해 정규화를 수행하여 레벨 비율과 레벨비율과 동일하게 분산을 맞춰준 스케일링된 방위각의 사인 값으로 구성된 새로운 공간 공분산 행렬 모델을 제안한다. 본 논문의 핵심적인 목적은 다음과 같다.
제안된 정규화된 공간 공분산 행렬의 초기화 과정의 적용을 통해 공간 모델의 추정 성능을 향상과 상향식 접근법에서의 같은 방향에 해당하는 추정된 소스들의 계층적 응집 클러스터링의 성능 향상을 통해 최종적인 분리된 음원의 품질을 향상시키는 것이다.
II. 기존 방법론
이 섹션은 본 논문의 기준선인 Sawada et al.[10]의MNMF를 소개한다. 본 논문에서는 행렬과 벡터에 관한 표기의 일관성을 위해 일반 소문자는 스칼라, 볼드체 소문자는 벡터, 볼드체 대문자는 행렬을 나타내고, 아래첨자 ab는 (a,b)번째 원소를 의미한다.
MNMF는 NMF의 한계인 실제 Short Time Fourier Transform(STFT)의 계수인 복소수를 다룰 수 없는 단점과 단일 채널의 STFT만 사용하므로 기저 행렬의 학습이 수반되어야 많은 소스와 잔향이 심한 어려운 환경에서의 분리성능이 보장된다는 단점[11] 등으로 인해 제안된 알고리즘이다.
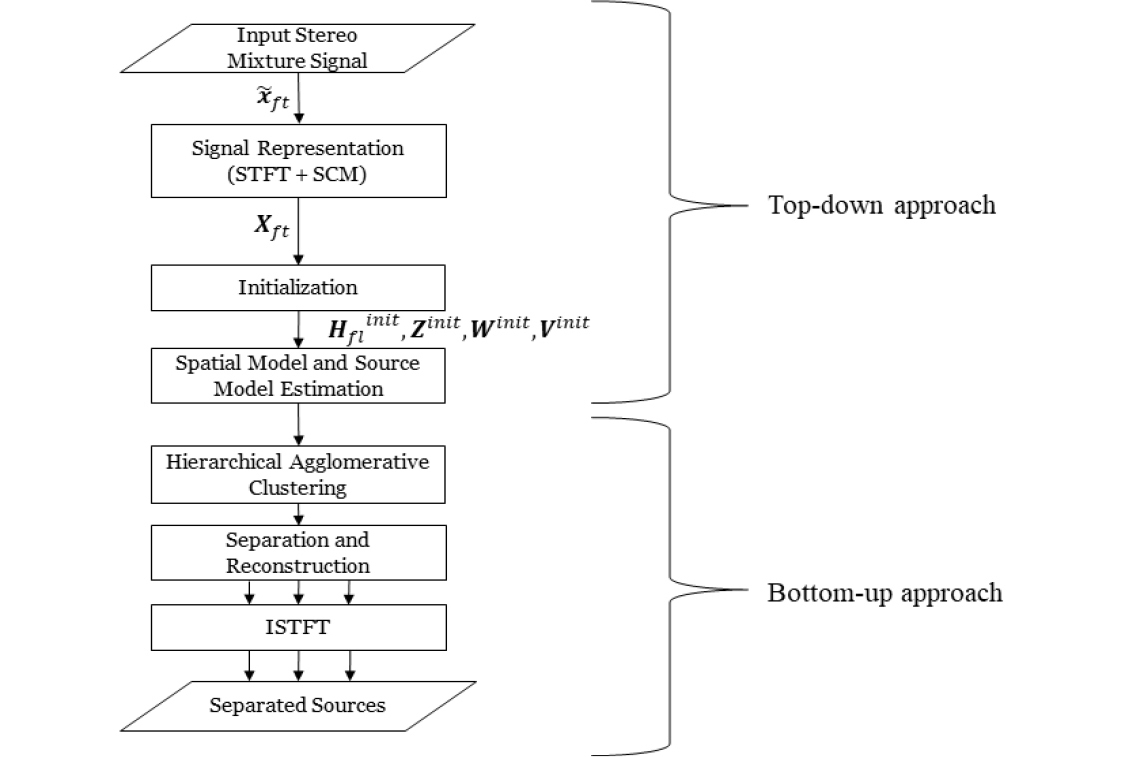
해당 알고리즘의 음원 분리의 전체적인 과정은 Fig. 2와 같이 크게 두 가지로 구분된다. 첫 번째로 하향식 접근법으로서 관찰된 혼합신호를 전처리과정을 통해 행렬로 변환한 입력행렬을 여러 행렬로 분해하는 과정이다.
두 번째는 상향식 접근법으로서 공간적인 정보를 바탕으로 여유 변수를 고려하여 초기 설정한 여러 추정된 소스 중에서 같은 방향에 해당하는 추정된 소스끼리 계층적 응집 클러스터링을 통해 실제 소스의 개수까지 순차적으로 통합하는 과정이다.
2.1 Top-down approach
하나의 마이크로 수음되는 신호의 파형 데이터를 STFT로 변환하면 주파수영역과 시간영역의 복소수의 성분으로 구성된 데이터를 얻을 수 있다. 마이크가 M개인 상황에는 그러한 는 M개가 존재하며 벡터로 표현하면 Eq. (1)과 같다.
| $${\overset{\boldsymbol\sim}{\mathbf x}}_{ft}=\begin{pmatrix}{\widetilde x}_{ft,1}\\\vdots\\{\widetilde x}_{ft,M}\end{pmatrix},$$ | (1) |
여기서 은 번째 주파수 빈, 번째 시간 축 프레임의 번째 마이크로폰의 STFT 데이터를 의미한다. Eq. (1)과 그 식을 켤레 전치를 취한 벡터를 서로 곱해주면 MNMF에 입력될 입력값에서 하나의 시간-주파수 요소는 최종적으로 Eq. (2)와 같이 구해진다.
여기서 의 대각성분은 각 채널의 파워이고 비대각성분은 각 채널끼리의 상관관계를 의미한다. 이 두 가지 공간적인 정보가 음원을 분리하는데 핵심적인 값이다.
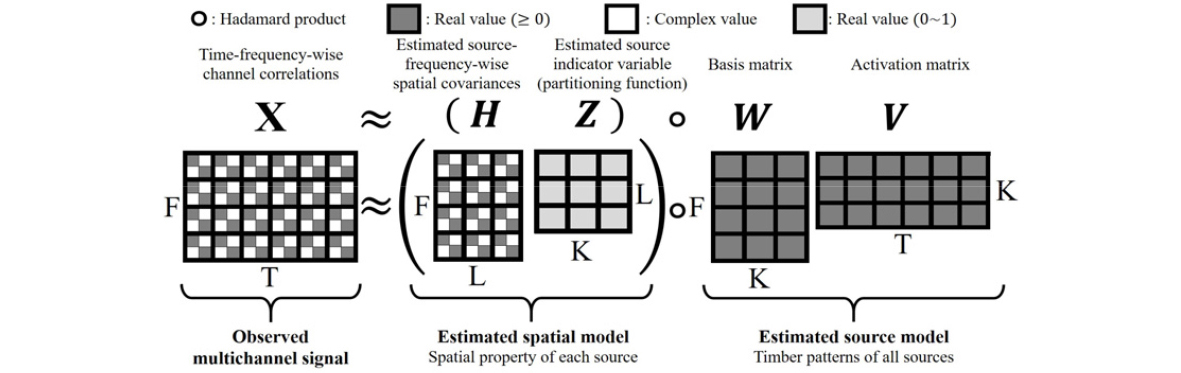
이러한 는 Fig. 3과 Eq. (3)과 같이 , , , 의 총 4개의 행렬로 분해가 가능하다. 는 의 슬롯에 공간 공분산 행렬이 포함된 복소수 행렬, 는 의 0에서 1사이의 실수 행렬 그리고 와 는 각각 , 의 비음수 실수 행렬이다. 여기서 는 주파수 빈의 개수, 은 추정된 소스의 개수, 는 NMF basis의 개수, 는 시간 프레임의 개수이다.
모델의 측면에서의 는 혼합신호를 분리하는데 사용될 공간 모델인 와 주파수와 시간 영역의 소스의 성분을 포함한 소스 모델인 로 나눌 수 있다.
공간 모델은 개별적인 추정된 소스마다 각 주파수 빈에 해당하는 공간 공분산 행렬을 포함한 와 같은 주파수 빈에서 어떤 추정된 소스의 공간 공분산 행렬이 지배적인지를 나타내는 로 구성되어 있다. 따라서 의 경우 을 만족한다.
소스 모델은 기존 NMF처럼 단일 채널의 비음수 스칼라 값으로써 주파수 영역의 행렬 와 시간영역의 로 구성되어 있다. 여기서 주의해야할 점은 와 를 아다마르 곱을 할 때 수치적인 크기의 모호성을 피하기 위해 의 경우 Eq. (4)의 unit-trace normalization과 의 경우 Eq. (5)의 unit-sum normalization이 수반되어야 한다.
마지막으로 각 행렬이 구성하는 값의 측면에서는 와 는 실수와 복소수로 구성되어 있으며, 는 0과 1사이의 실수값 그리고 와 는 양의 실수값으로 구성되어 있다.
| $${\widehat{\boldsymbol X}}_{ft}=\sum_{k=1}^K\left(\sum_{l=1}^L{\boldsymbol H}_{fl}z_{lk}\right)w_{fk}v_{kt,}$$ | (3) |
여기서 는 NMF basis의 개수, 은 추정된 소스의 개수이다.
| $$(HZ)_{fk}\leftarrow(HZ)_{fk}/tr(HZ)_{fk}.$$ | (4) |
| $$z_{lk}\leftarrow z_{lk}/(\sum_l^Lz_{lk}).$$ | (5) |
그러한 4개의 행렬을 업데이트하는 수식은 와 의 차이를 구하는 여러 발산 방법론 중에 모든 주파수에서 동일한 발산이 구해지며 음원에 적절한 방법인 Itakura-Saito(IS) divergence와 multiplicative Update Rules를 활용하면 구할 수 있으며 Eqs. (6) ~ (11)과 같이 각 행렬을 업데이트한다.
특히 를 업데이트하기 위해서는 Eq. (9)의 Ricatti 방정식을 고유값 분해와 에르미트 행렬의 성질을 활용하여 구해야 한다. 자세한 내용은 Sawada et al.[10]의 MNMF를 참고하기 바란다.
| $$H_{fl}AH_{fl}=B,$$ | (9) |
여기서
| $$A= \sum _{k} ^{} z _{lk} w _{fk} \sum _{t} ^{} v _{kt} {\hat{X}} _{ft} ^{-1},$$ | (10) |
| $$B=H_{fl}'(\sum_k^{}z_{lk}w_{fk}\sum_t^{}v_{kt}\widehat X_{ft}^{-1}X_{ft}\widehat X_{ft}^{-1})H_{fl}'.$$ | (11) |
2.2 Bottom-up approach
Top-down approach를 통해 개별 행렬인 가 잘 추정이 되었다면, 다음으로 bottom-up approach를 수행한다. 즉, 개별적인 소스 분리를 위해 같은 방향의 추정된 소스들을 클러스터링 해야 한다.
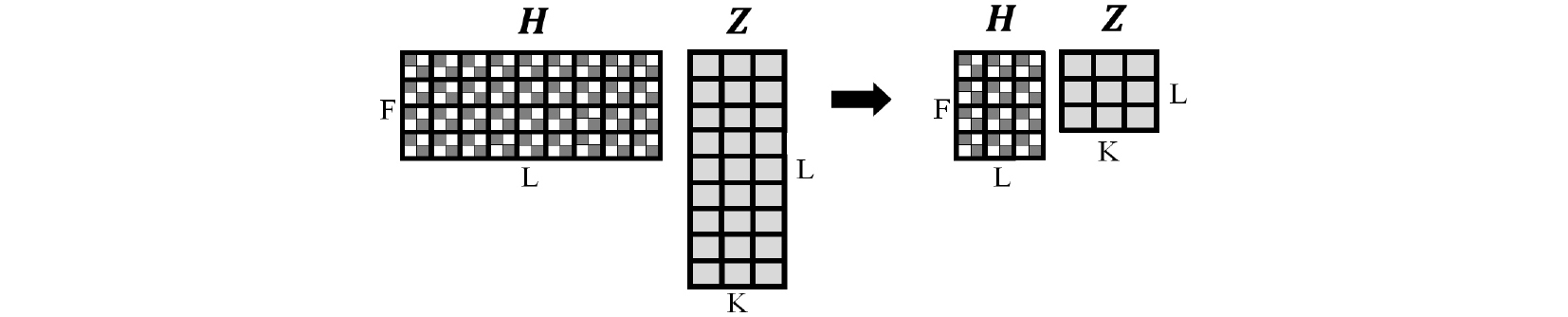
그러한 목표에 대한 핵심적인 행렬은 추정된 소스-주파수 슬롯마다 공간 공분산 행렬을 포함한 와 개별 추정된 소스의 상대적인 비율에 대한 행렬인 이다. 따라서 Fig. 4와 같이 순차적인 수행마다 내의 L개 추정된 소스들의 가능한 모든 조합에 대해 Eq. (12)를 통해 거리를 구해서 실제 소스의 개수에 도달할 때까지 가장 가까운 추정된 소스 쌍을 Eqs. (13) ~ (15)를 통해 요소별 가중치 평균을 구하여 하나씩 줄여가는 계층적 응집 클러스터링을 수행한다. Eq. (12)는 개별 주파수 빈에 대해 frobenius norm을 구해서 주파수 빈에 대해 모두 더한 거리가 두 추정된 소스의 거리가 되는 수식이다.
| $$d_{\boldsymbol H}(l_1,l_2)=\sum_{f=1}^F\parallel{\boldsymbol H}_{fl_1}-{\boldsymbol H}_{fl_2}\parallel_{Frobenius},$$ | (12) |
여기서 는 주파수 빈의 개수이다.
| $${\boldsymbol H}_{fl_{new}}=\frac{\omega_1\times{\boldsymbol H}_{fl_1}+\omega_2\times{\boldsymbol H}_{fl_2}}{\omega_1+\omega_2},$$ | (13) |
여기서 는 가장 가까운 추정된 소스 쌍을 합친 새로운 추정된 소스이며,
| $$\omega_1=\sum_{k=1}^Kz_{l_1k},\;\omega_2=\sum_{k=1}^Kz_{l_2k}.$$ | (14) |
| $$z _{l _{new} k} =z _{l _{1} k} +z _{l _{2} k}.$$ | (15) |
Bottom-up approach에서 각 소스의 방향에 해당하는 추정된 소스가 잘 클러스터링이 되었다면 마지막으로 개별 추정된 소스에 해당하는 STFT를 Eq. (16)과 같이 Wiener filter를 통해 구하고 inverse STFT를 취해주면 최종적인 파형 데이터의 음원을 얻을 수 있다.
| $${\widetilde{\boldsymbol y}}_{ft}^{(l)}=\left(\sum_{k=1}^Kz_{lk}w_{fk}v_{kt}\right){\boldsymbol H}_{fl}{\widehat{\boldsymbol X}}_{ft}^{-1}{\widetilde{\boldsymbol x}}_{ft}.$$ | (16) |
III. 제안된 방법론
3.1 문제 정의
본 섹션에서는 기존 방법론에서 공간 공분산 행렬의 단점을 분석한다. 실제로 수많은 채널에 적용가능한 알고리즘이지만 연산시간과 관련된 실용적이며, 본 연구의 시뮬레이션과 실험과 같은 조건인 두 개의 마이크로 수음되는 신호를 다루기 위해 2채널 신호에 대한 행렬을 바탕으로 이론과 실험을 설명할 것이다. 따라서 이 2가 되며 공간 공분산 행렬이 2×2행렬이 된다.
기존 공간 공분산 행렬의 요소들은 같은 방향에 대해 서로 다른 값을 가지는 상황이 발생할 수 있는 단점이 있다. 그 이유는 행렬의 대각성분의 경우 제한 없이 매우 큰 값이 존재할 수 있으며 클러스터링 기법에 취약한 조건인 특이치에 의해 성능이 저하될 수 있는 단점이 있다.
비대각성분은 주파수에 매우 의존적이어서 같은 방향에 여러 주파수로 구성된 추정된 소스가 존재한다면 각 주파수별 위상차는 서로 다른 값을 가진다.
3.2 Normalized Spatial Covariance Matrix
본 섹션에서는 상향식 접근법에서 각 추정된 소스간의 거리를 보다 더 잘 구할 수 있으며 공간 모델을 구성하는 와 의 초기값에 활용 가능한 정규화된 공간 공분산 행렬을 제안한다.
본 연구에서는 발견한 단점을 개선하기 위해 같은 방향에서 동일한 값을 가지도록 어떤 특징값을 활용해야할지 고민하였다. 이를 위해 클러스터링 기법을 활용하여 서로 다른 방향의 소스를 분리시킨다는 관점에서 클러스터링에 관한 여러 연구들을 살펴보았다.
여러 연구 중에서 Sawada가 속한 NTT그룹에서 방향성을 가지는 다양한 특징값들에 대한 클러스터링 성능을 분석해 놓은 연구가 있었다.[12] 해당 연구를 바탕으로 가장 클러스터링 성능이 높은 특징값인 Eq. (17)을 선택 및 활용하였다.
여기서 d는 마이크의 간격이며 c는 음속이다.
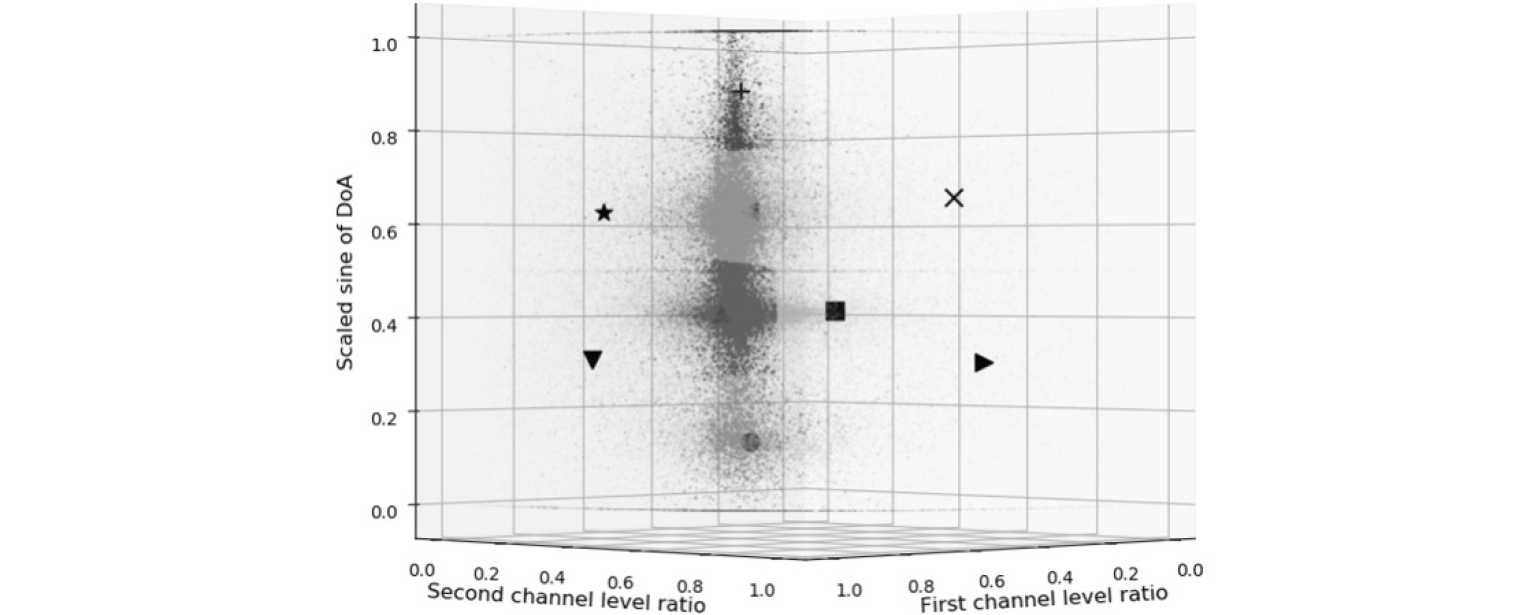
처음 두 개의 성분은 각 채널의 정규화된 레벨의 비율이다. 단일 채널의 크기를 전체 채널의 크기에 해당하는 값으로 나눠줌으로써 채널의 크기에 관계없이 같은 방향에 대해서는 동일한 값이 도출되며 특이치에 대해 더 이상 취약하지 않다. 예를 들자면, 같은 방향에 소스를 구성하는 여러 추정된 소스가 존재하는데 개별 추정된 소스마다 크기가 다르더라도 모든 채널에서의 해당 채널의 비율이므로 동일한 값이 나온다.
마지막 성분은 먼저 Eq. (18)과 같이 두 신호의 켤레곱의 편각을 구하여 Eq. (19)의 와 같은 Phase difference of Arrival(PdoA)를 구하고, 이를 각주파수로 나눠주어 주파수 의존성을 없애고 Eq. (20)의 와 같이 Time difference of Arrival(TdoA)를 구한다. 마지막으로 시간의 차이에 음속과 마이크 사이의 거리를 고려하여 Eq. (21)과 같이 최종적인 Sine of Direction of Arrival(Sine of DoA)인 의 값으로 구한 것이다.
본 논문에서는 실제 공간 공분산 행렬의 정규화 수행시 레벨의 비율의 분산과 맞춰주어 동일한 가중치를 주기 위해서 Eqs. (22) ~ (23)의 비대각 성분과 같이 에 1을 더한 값을 2로 나누어 동일한 범위인 0과 1 사이의 분산을 가지도록 새롭게 특징값을 구성하였다.
따라서 의 정규화를 통해 Eq. (22)와 의 정규화를 통해 Eq. (23)을 제안하였다.
| $$\triangle\tau(f,t)_{1,2}=\frac{d\times\sin(\theta(f,t)_{1,2})}c=\frac1{2\pi f}\triangle\Phi(f,t)_{1,2}=\frac1{2\pi f}\arg\lbrack{\widetilde x}_{ft,1}\widetilde x_{ft,2}^\ast\rbrack.$$ | (20) |
| $$sin(\theta(f,t)_{1,2})=\frac{c\triangle\tau(f,t)_{1,2}}d=\frac1{2\pi fc^{-1}d}arg\lbrack{\widetilde x}_{ft,1}\widetilde x_{ft,2}^\ast\rbrack.$$ | (21) |
이로써 같은 방향에 대해 동일한 값을 가지는 공간 공분산 행렬을 새롭게 제안함으로써 분리된 개별 소스의 방향성의 성능이 향상될 것이며 결과적으로 음원을 분리하는 데도 큰 이점이 있을 것을 기대할 수 있다.
3.3 정규화된 공간 공분산 행렬의 적용
본 알고리즘에서 정규화된 공간 공분산 행렬을 활용 가능한 부분은 두 가지이다. 첫 번째는 와의 행렬의 초기값에 활용가능하고 두 번째는 첫 번째 과정을 통해 하향식 접근법에서 보다 더 잘 추정한 에서 Hierarchical Agglomerative Clustering(HAC)를 효과적으로 수행함으로써 궁극적인 음원의 분리성능을 향상시키는 것이다.
3.3.1 와 의 초기값에 활용되는 정규화된 공간 공분산 행렬
기존 방법론을 비롯한 MNMF를 기반으로 하는 여러 연구에서 초기값에 민감하다는 점을 언급하고 있다.[10], [13] 실제로 공간 모델에 대한 여러 연구가 진행되어 오고 있다.[14]
기존 방법론의 초기화과정에서는 의 경우 모든 추정된 소스-주파수 슬롯에 대각 성분을 , 비대각 성분은 0으로 고정된 값으로써 초기화 한다.[14]의 경우에는 모든 요소에 대해 에 근접한 값으로 초기화 한다.[14] 즉, 모든 추정된 소스 각각에 대해 정중앙에 거의 동일한 비율로 형성된 음원으로 가정하는 것이다.
이러한 초기값을 개선하기 위해 관찰된 혼합신호인 를 정규화한 를 바탕으로 모든 4차원의 데이터가 주파수와 시간에 무관하게 같은 방향에서 같은 성분을 가지도록 변환함으로써 비교가능하게 구성한다. 이러한 데이터들의 분포를 통해 ‘K-means 클러스터링’기법으로 Fig. 5와 같이 의 추정된 소스 개수와 동일한 L개의 추정된 소스의 중심인 를 구할 수 있고 의 각 원소를 Eq. (24)와 같이 다시 기존의 에 대응되는 주파수별 역연산을 취해주면 반복수행을 하는 관점에서 보다 더 좋은 시작점으로 을 잘 추정할 수 있다.
다시 말하면, 추정한 L개의 클러스터의 중심이 대략적인 추정된 소스들의 위치값으로서 의 공간 공분산 행렬의 값과 대응되며 의 초기값이 목적이므로 하향식 접근법을 수행하기 위해 에 대응되는 값으로 Eqs. (19) ~ (21)을 바탕으로 역연산을 수행한 것이 Eq. (24)이다. 의 경우에는 Eq. (25)와 같이 각 추정된 소스에 존재하는 데이터의 개수와 그 크기의 연산을 통해 모든 데이터의 합은 1을 바탕으로 하는 각 클러스터의 상대적인 비율을 정한다.
따라서 본 알고리즘은 적응 방법론처럼 분리하고자 하는 혼합 음원인 입력데이터마다 확률론적으로 클러스터링을 통해 대략적인 음원의 위치를 처럼 실제 음원개수보다 훨씬 많이 설정하여 HAC에서 줄여가기 때문에 효과적으로 활용될 수 있는 방법론이다.
음원의 설정 개수가 줄어든다면 각 클러스터의 중심점의 관점에서 각도의 분해능이 줄어들며 오차가 발생 가능성과 상향식 접근법에서도 클러스터링 수행 시 중요한 클러스터를 놓칠 수 있으므로 Sawada가 경험적으로 제안한 실제 소스 개수의 3배로 정한다.[10]
| $$z_{lk}^{init}=\frac{\displaystyle\sum_{f,t}^{}tr(\boldsymbol X_{ft}^{(l)})}{\displaystyle\sum_{f,t,l}^{}tr(\boldsymbol X_{ft}^{(l)})}.$$ | (25) |
3.3.2 Bottom-up approach에서의 HAC에 활용되는 개선된 거리 행렬
Bottom-up approach의 전체적인 과정에서 다른 점은 기존 을 정규화하는 과정과 여러 추정된 소스들의 조합 중에서 가장 가까운 추정된 소스 쌍을 구하는 과정에 을 활용하여 최적의 클러스터링을 위한 과정을 추가하였다. 뿐만 아니라 제안된 정규화된 공간 공분산 행렬은 모든 주파수 빈에 대해 같은 방향에 대해 동일한 값을 가지므로 평균을 취해서 두 추정된 소스 쌍의 거리를 구하는 Eq. (26)과 같은 새로운 거리함수를 제안한다.
| $$d_{\boldsymbol Q}(l_1,l_2)={\left\|\frac{{\displaystyle\sum_{f=1}^F}{\boldsymbol Q}_{fl_1}}F-\frac{{\displaystyle\sum_{f=1}^F}{\boldsymbol Q}_{fl_2}}F\right\|}_{Frobenius}.$$ | (26) |
IV. 실 험
본 실험은 기준 데이터셋과 객관적인 평가 도구인 BSS Eval toolbox를 활용하여 분리 성능을 검증한다.[15] 이 검증도구는 추정된 소스들과 실제 소스들을 입력해 주었을 때 4가지 성능 지표를 출력으로 구할 수 있는 매우 객관적인 검증 도구이다.
첫 번째 지표는 신호에 대한 왜곡의 성분을 분석하는 Signal to Distortion Ratios(SDR)이며, 두 번째는 소스끼리의 간섭에 대한 지표인 Source to Interference Ratios(SIR), 세 번째는 의도치 않은 인위적인 성분에 대한 지표인 Sources to Artifact Ratios(SAR), 마지막으로 소스 이미지의 방향에 대한 왜곡에 대한 성분인 Source Image to Spatial distortion Ratio(ISR)로 구성되어 있다.
4.1 실험 조건
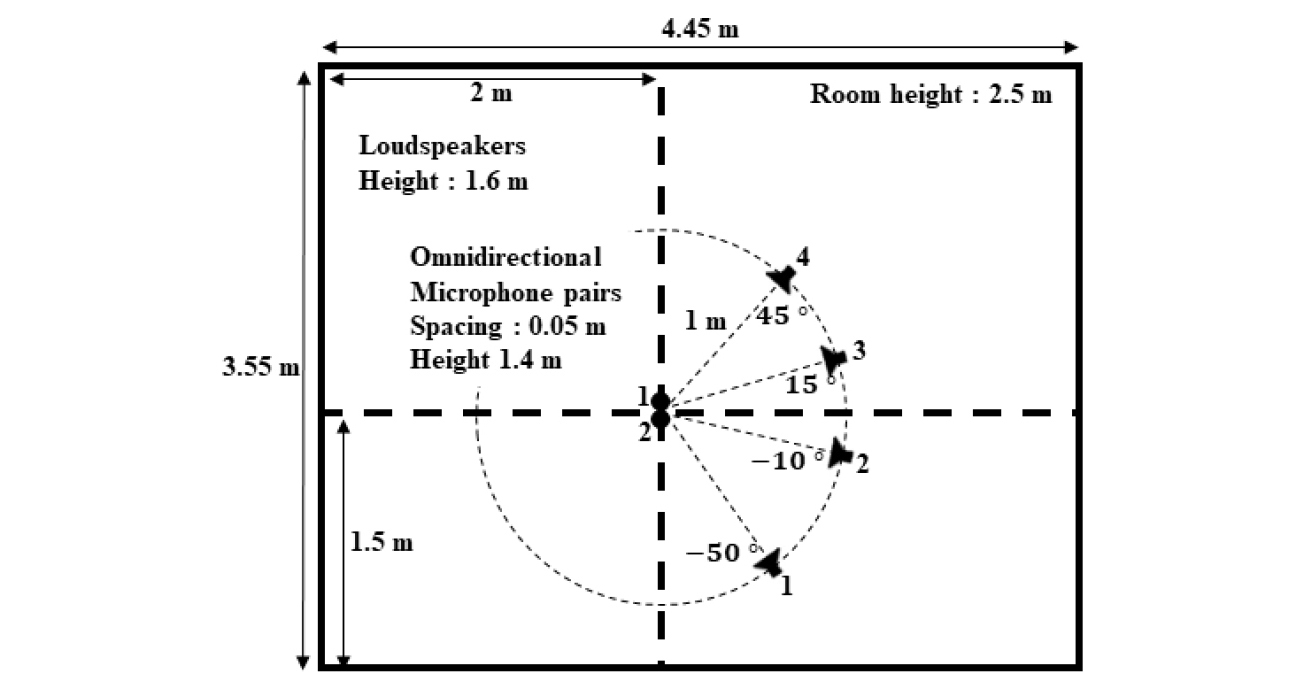
본 실험의 조건은 Tables 1, 2와 Fig. 6과 같은 조건에서 전문적으로 생성한 Signal Separation Evaluation Campaign(SiSEC) 2008 데이터셋에 적용하였다.[16]
Table 1. Experiment conditions.
Table 2. Underdetermined speech and music mixtures.
이 논문에서는 그 중 ‘under-determined speech and music mixtures’에 있는 첫 번째 development 데이터셋(dev1.zip)을 활용한다. 또한 여러 혼합조건 중에 ‘Live recordings’와 가장 어려운 잔향 조건인 250 msec의 잔향시간(RT60)의 데이터를 활용한다. ‘Live recordings’ 조건은 Fig. 6과 동일한 실내 조건에서의 실제 녹음된 혼합 신호이다.
4.2 실험 결과
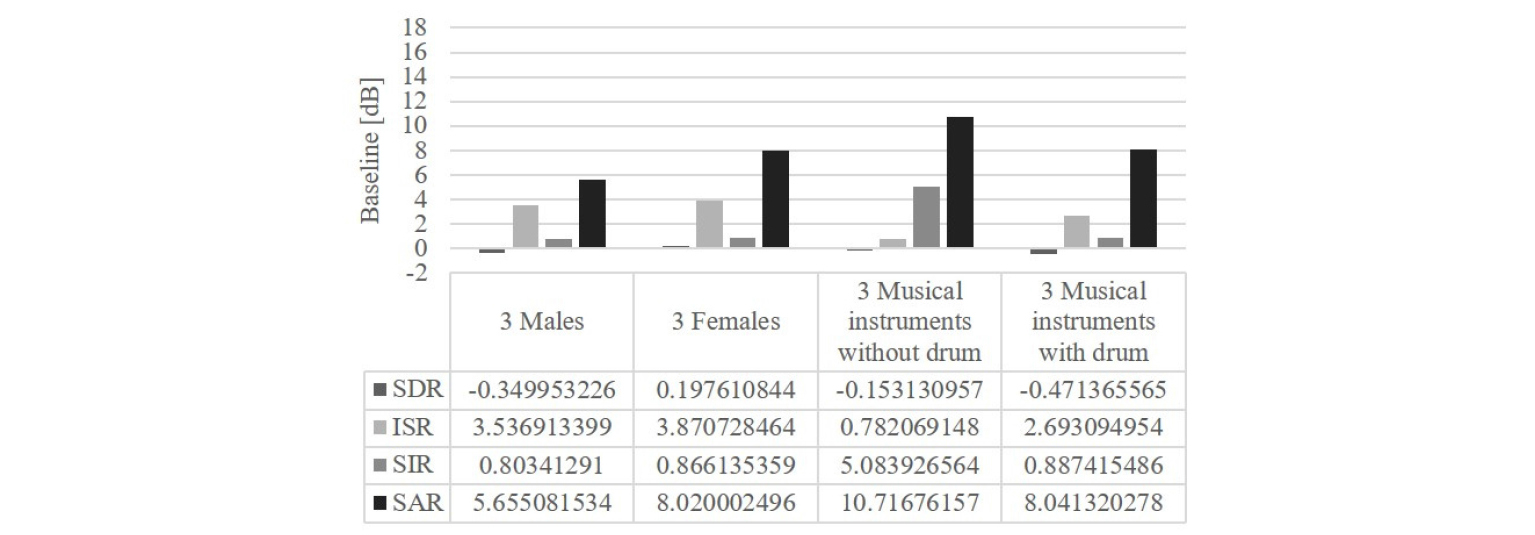
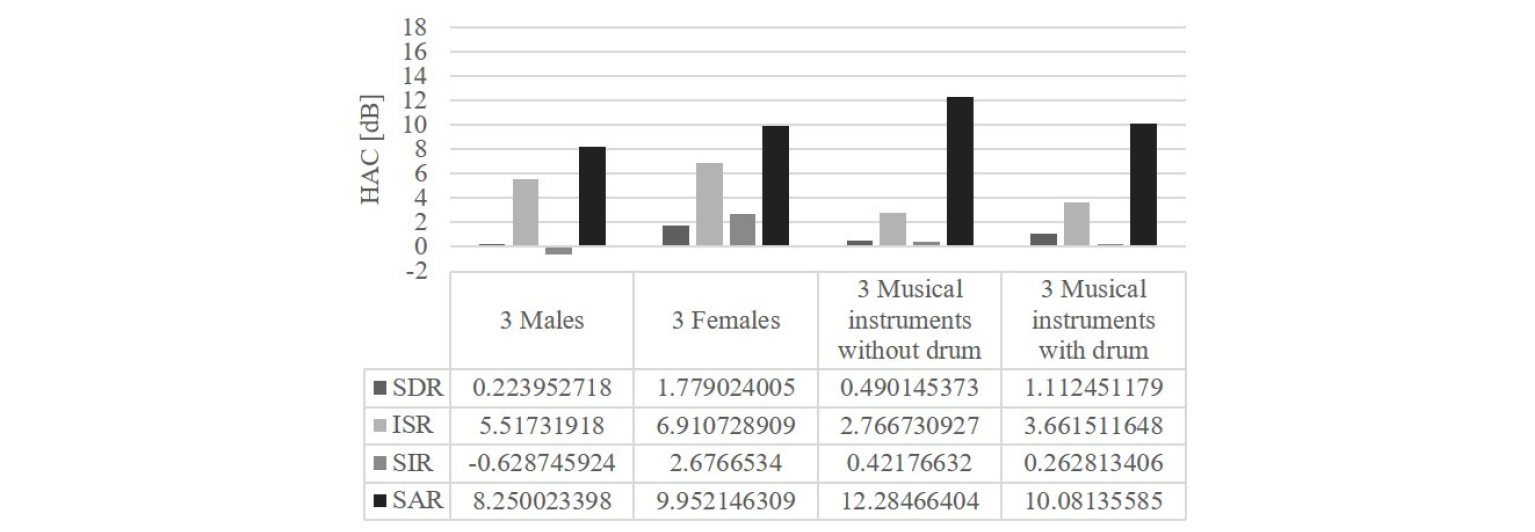
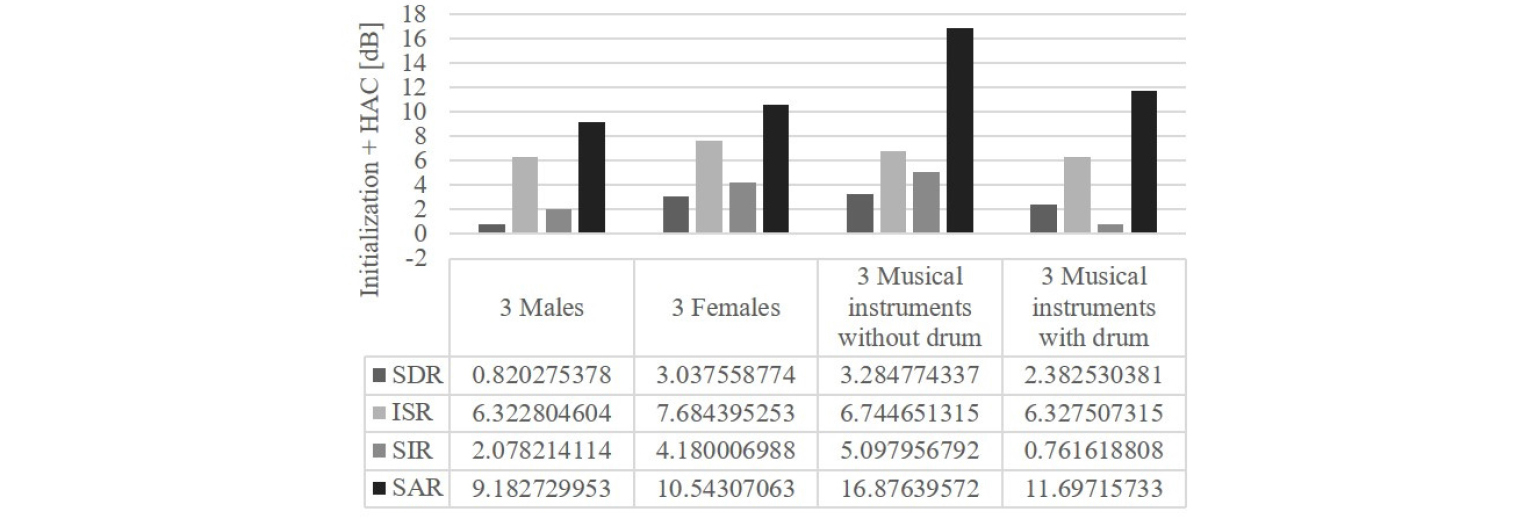
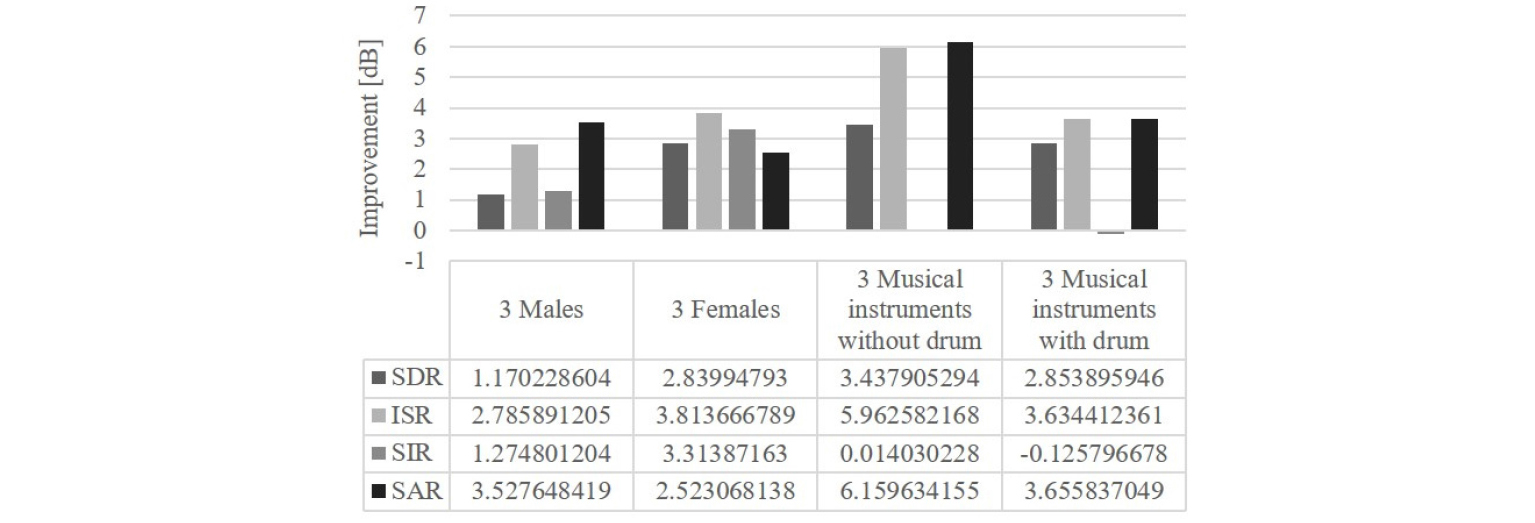
BSS Eval Toolbox를 활용하여 모든 실험 데이터셋에 대해 실험을 해보았을 때의 정량적인 수치는 다음과 같다. Fig. 7은 기존 방법론의 수치이며 Fig. 8은 계층적 응집 클러스터링(HAC)만 적용한 결과, Fig. 9는 초기값과 HAC 모두 적용한 제안된 방법의 결과 그리고 Fig. 10은 최종적으로 기존 방법론 대비 향상된 수치를 나타낸 것이다.
여기서 제안된 HAC와 초기값 알고리즘의 영향력 및 효과를 수치적으로 확인해보면 HAC의 경우에는 Fig. 8에서 확인가능하며 방향에 대해 올바르게 클러스터링 했다는 점에서 추측한 대로 ISR이 큰 폭으로 상승하였으며 다른 수치들도 소폭 상승하였다. 그리고 초기값 알고리즘의 경우에는 Figs. 8과 9를 비교해 보았을 때 SDR과 SIR에 해당하는 수치가 큰 폭으로 상승했으며 나머지 수치는 소폭 상승한 것으로 보아 정중앙이 아닌 대략적인 위치의 시작점에서 개별 추정된 소스의 시작점을 정해줌으로써 다른 소스와의 간섭에 강건해짐을 확인할 수 있었다.
따라서 최종적인 성능 향상에 대한 그래프인 Fig. 10에서 확인할 수 있듯이 모든 혼합신호에 대해 대부분의 성능지표가 향상되는 것을 확인할 수 있다. 악기로 구성된 음악의 경우에는 유독 SIR에서 성능이 거의 변동이 없는 것으로 보이는데 이는 악기의 성분 특성이 여러 시간에 대해 매우 유사한 음색과 패턴을 가지고 있어 서로 잘 동기화되는 성질이 있기 때문이다.[17] 즉, sparseness based approach의 가설에 어려운 상황이 발생한다는 점이다. 이에 비해 음성은 계속해서 동적으로 변하기 때문에 간섭이 덜 발생하였다.
이러한 제안된 알고리즘의 연산 시간과 수렴 성능을 파악하기 위해 기존 방법론과 동일한 iteration을 수행하여 비교하였다. 본 알고리즘은 Intel Core i7- 4790(3.60GHz) CPU 프로세서에서 실행하였다.
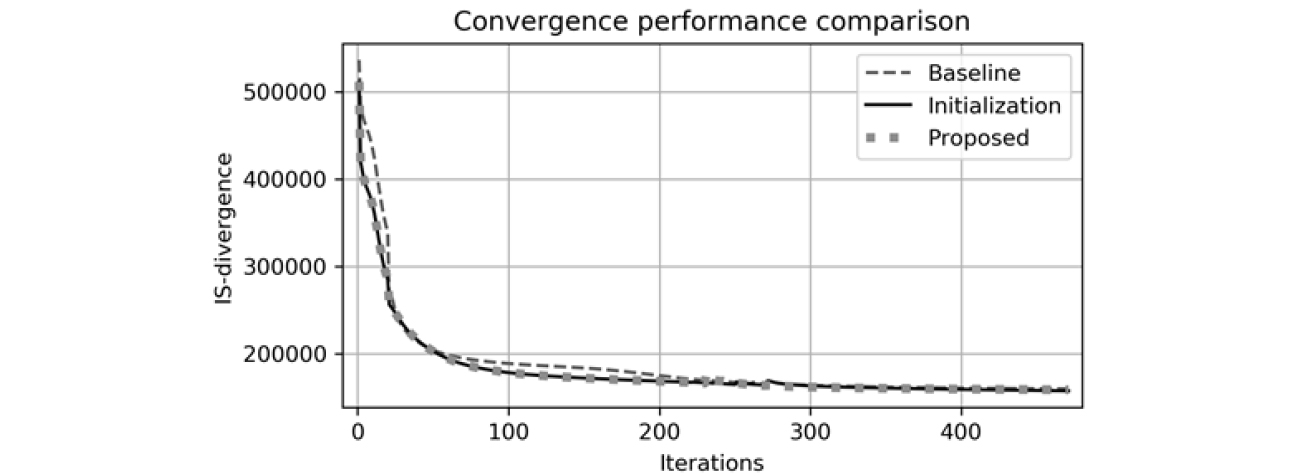
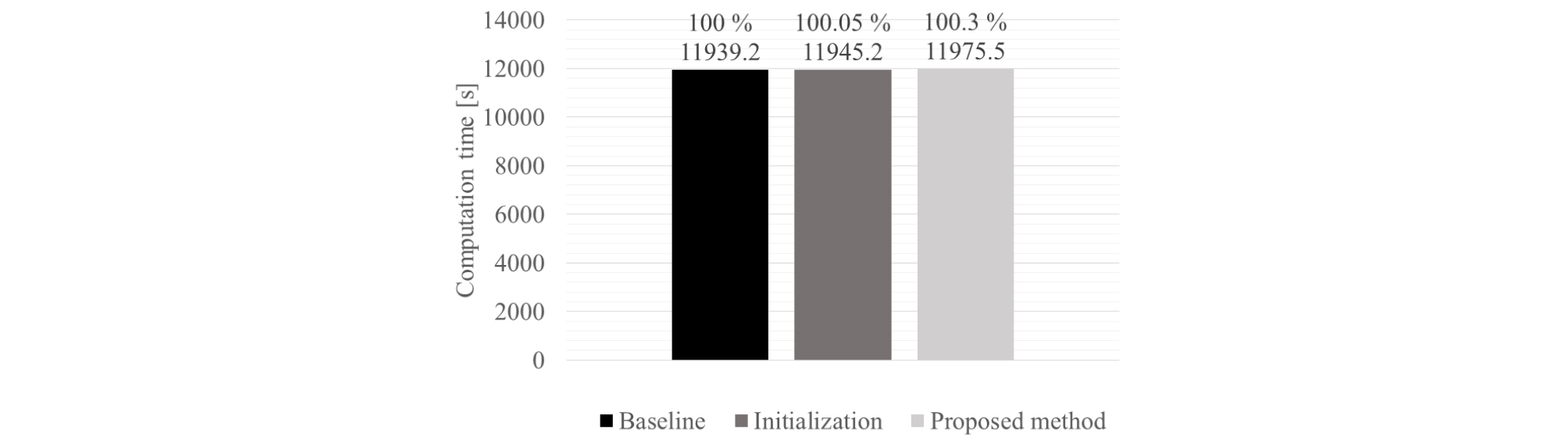
수렴 성능의 경우 Fig. 11처럼 기존 방법론 대비 제안된 두 방법론에서 보다 더 빠르게 수렴하며 발산 또한 더 작은 값을 가지므로 성능 우위가 있음을 확인하였다. 연산 시간의 경우에는 Fig. 12처럼 기존 방법론과 비교하였을 때 초기값 알고리즘의 경우에는 연산시간이 소폭 상승하였지만 제안된 모든 방법을 적용하였을 때는 보다 더 크게 상승하였다.
모든 알고리즘을 적용하였을 때 연산시간이 더 크게 상승한 이유는 실제 상향식 접근법에서 모든 시간 프레임과 주파수 빈에서의 하나의 슬롯에 해당하는 공간 공분산 행렬을 모두 매 iteration마다 정규화를 수행하기 때문이다. 하지만 초기값 알고리즘은 입력 행렬에 대해 한번만 수행하면 되므로 소폭 상승하였다.
전체연산을 고려하였을 때 늘어난 시간은 0.3 %이내이므로 제안된 알고리즘의 효용성을 재확인하였다.
V. 결 론
본 연구에서는 음원분리에 있어 어려운 상황인 underdetermined convolutive situation에서 BSS분야에서 널리 활용되며 모든 상황의 음원에 적용 가능한 실용적인 MNMF의 개선점을 파악하고 새로운 아이디어 구체화를 통해 적용한 결과 다음과 같은 결론을 얻었다.
1. 기존 알고리즘인 Sawada’s MNMF을 비롯한 여러 MNMF의 단점인 초기값에 민감하다는 점에서 MNMF의 공간 모델에 해당하는 와 의 대략적인 시작점을 지정함으로써 입력 데이터에 관계없이 어떠한 혼합신호에도 적용이 가능한 적응형 알고리즘을 개발하였고 성능을 검증하였다.
2. Bottom-up approach에서의 HAC에 활용되는 와 효과적인 거리함수를 통해 최적의 HAC를 수행함으로써 성능을 크게 향상시켰다.
3. 기준 데이터셋과 객관적인 검증 도구인 BSS eval toolbox를 활용함으로써 성능 향상 및 비교 우위를 직관적으로 파악할 수 있도록 설계하였고 성능을 검증하였다.
향후 연구는 다음과 같다. GPU의 활용과 joint diagonalization을 기반으로 한 FASTMNMF 알고리즘을 통해 음원분리알고리즘의 연산 및 수렴속도를 높이고 실시간으로 활용 가능한 실용적인 알고리즘 접목에 대한 연구를 수행할 것이다.[5], [18]