I. 서 론

압축 센싱은 최근 주목 받고 있는 신호 처리 기법이다. 압축 센싱의 기본 원리는 복원하려는 신호의 차원이 관측된 신호의 차원보다 큰 경우에도 관측된 신호로부터 원 신호를 복원할 수 있다는 것이다. 복원을 위해서는 두 가지 조건이 필요하다. 복원하려는 신호가 특정 도메인에서 충분히 희소한 벡터여야 한다는 것과 센싱 행렬이 RIP(Restricted Isometry Property) 조건을 만족시키는 충분히 비간섭적인 행렬이어야 한다는 것이다.^{[1], [2]}

능동 소나의 거리 도플러 추정에서 압축 센싱의 기본 원리에 대한 두 가지 조건을 확인할 수 있다. 능동소나에서 탐지해야 하는 표적의 정보는 표적의 개수만큼 존재한다. 탐지를 위해 고려하는 여러 잠재적 표적 정보들 중에서 실제 표적의 정보는 충분히 희소하다. 또한 능동소나의 송신 신호에 시간 지연과 도플러 천이를 적용하여 잠재적 표적이 될 수 있는 여러 복제 신호를 생성할 수 있는데, 각 복제 신호를 열벡터로서 나열하여 만든 센싱 행렬은 RIP조건을 만족 시키도록 설계할 수 있다. 따라서 능동소나의 표적 탐지에 압축 센싱을 적용할 수 있으며, 압축 센싱 알고리즘을 통해 능동 소나의 수신 신호로부터 표적의 거리 도플러 정보를 추정할 수 있을 것이다.

압축 센싱을 적용한 거리 도플러 탐지 방식은 세 가지 변수에 의해 추정 성능이 좌우된다. 신호 대 잡음비 값, 센싱 행렬의 상호간섭성 값과 사용한 압축 센싱 알고리즘이 이에 해당된다. 신호 대 잡음비는 수신 신호에 잡음이 섞여 들어간 정도의 비율을 나타내는 지표이고, 센싱 행렬의 상호 간섭성은 송신 신호로부터 생성한 여러 잠재적 표적의 정보를 나타내는 복제 신호들 간의 유사도를 나타내는 지표이다. 또한 사용한 압축 센싱 알고리즘에 따라 수신 신호로부터 구한 표적의 거리 도플러 정보의 추정치가 달라질 수 있다.

현재 능동 소나에 압축 센싱 기법을 적용한 많은 연구가 진행 중에 있지만, 압축 센싱을 능동 소나의 거리 도플러 탐지에 적용한 사례는 많지 않으며, 특히 여러 조건하에서 달라지는 추정성능의 비교에 대한 연구는 아직 수행되어 있지 않다.

본 논문에서는 신호 대 잡음비 값과 센싱 행렬의 상호 간섭성 값의 변화에 따른 여러 압축 센싱 알고리즘의 계산 성능, 정확도를 확인한다. 이를 바탕으로 특정 신호 대 잡음비 값, 특정 상호 간섭성 값을 갖는 상황에서 최고의 성능을 나타낼 수 있는 최적의 알고리즘을 확인한다.

II장에서는 거리-도플러 신호의 모델을 제시하였다. III장에서는 본 논문에서 다룰 네 가지 압축 센싱 알고리즘을 소개한다. IV장에서는 III장에서 소개한 압축 센싱 알고리즘을 사용하여 각 알고리즘의 계산성능, 정확도에 대해 모의실험을 한 결과를 제시했다. V장은 결론이다.

II. 거리-도플러 신호 모델

본 논문에서는 능동 소나의 송신신호로서 LFM (Linear Frequency Modulation) 신호를 사용하였다. 기저 대역의 LFM 신호는 다음과 같다.

여기서$T$ 는 펄스의 주기이며, $\alpha$는 주파수 변화율이다. 송신 신호 $s\left(t\right)$에 아래와 같은 시간 지연과 도플러 천이를 적용함으로써 잠재적 표적으로부터 반사된 신호 $r\left(t\right)$를 생성할 수 있다.

여기서 $\tau ,f_d$ 는 각각 지연 시간, 도플러 주파수이다. 여러 개의 시간 지연 빈(bin)과 도플러 빈을 줌으로써 여러 잠재적 표적 신호를 생성할 수 있다. $P$개의 시간 지연 빈과 $Q$개의 도플러 빈을 주고, $r\left(t\right)$를 샘플링 주파수 $f_s$로 샘플링한 신호 $r_{p,q}\left[n\right]$은 다음과 같이 표현된다.

모호함수의 에일리어싱을 피하기 위해 최대 도플러 주파수가 샘플링 주파수를 넘지 않도록 하였다. Eq. (3)을 열벡터로 나열하여 생성한 센싱 행렬은 다음과 같다.

위의 센싱 행렬을 이용하여 거리-도플러 신호 모델을 구성하면 다음과 같다.

센싱 행렬 $A$를 $M\times N$차원 행렬이라 하면, $b$는 $M$차원인 능동 소나의 관측된 수신 신호 벡터이며, $x$는 표적의 반사계수를 의미하는 $N$차원 벡터이다. $e$는 $M$차원의 소음 벡터이다. 여기서 $M$은 $T{f}_s+P$ 이며, $N$은 $PQ$이다. $M<N$ 인 경우에 Eq. (5)의 해는 무수히 많지만, 표적의 반사 계수인 $x$가 희소하다는 조건을 부여할 때, 압축 센싱 알고리즘을 적용하여 유일 해를 구할 수 있다.

III. 압축 센싱 알고리즘

본 논문에서 다룰 압축 센싱 알고리즘은 OMP(Orthogonal Matching Pursuit), CoSaMP(Compressive Sampling Matching Pursuit), BPDN(CVX)^[10](Basis Pursuit Denoising), LARS(Least Angle Regression) 알고리즘이다. 이중 OMP, CoSaMP 알고리즘은 greedy 알고리즘 기반의 l₀-norm 최소화 방식에 해당되고, BPDN(CVX), LARS 알고리즘은 최적화 이론 기반의 l₁-norm 최소화 방식에 해당된다. 위의 두 가지 최소화 방식을 소개한 후에 l₀-norm 최소화 방식에 해당하는 OMP, CoSaMP 알고리즘을 각각 3.1, 3.2절에서 다루고, l₁- norm 최소화 방식에 해당하는 BPDN(CVX), LARS 알고리즘은 각각 3.3, 3.4절에서 다룬다.

II장에서 기술하였듯이 기본적으로 압축 센싱이 다루는 Eq. (5)는 과소 결정 시스템이다. 과소 결정 시스템의 해는 무수히 많거나 존재하지 않는다. 해가 무수히 많은 경우에 정규화를 통해 원하는 해를 도출할 수 있다. 압축 센싱 알고리즘은 Eq. (5)에 정규화 과정을 적용하여 가장 희소한 해를 도출한다. 압축 센싱 알고리즘의 정규화 방식은 크게 두 가지로 분류할 수 있다. 첫 번째는 greedy 알고리즘 기반의 l₀-norm 최소화 방식이고, 두 번째는 최적화 이론 기반의 l₁-norm 최소화 방식이다.^[3] 소음이 존재할 경우에 위의 두 가지 최소화 방식을 수식으로 표현하면 다음과 같다.

여기서 $\epsilon$은 Eq. (5)의 e의 영향을 반영하여 허용된 오차 범위이다. $\epsilon$은 보통$\parallel e{\parallel }_2^2={ϵ}^2$을 만족하도록 설정한다. l₀-norm은 비볼록 함수인 반면에 l₁-norm은 볼록 함수이다. 따라서 Eq. (7)의 l₁-norm 최소화 방식은 볼록 최적화를 통해 선형 프로그래밍으로 해를 도출 하지만 Eq. (6)의 l₀-norm 최소화 방식은 greedy한 특성을 기반으로 해를 도출한다.

3.1 OMP 알고리즘

l₀-norm 최소화 방식의 대표적인 알고리즘인 OMP의 과정은 Table 1과 같다. OMP 알고리즘은 매 반복 과정 마다 잔차 벡터와의 상관도가 가장 높은 한 개의 열벡터를 선택하며 진행된다. 선택된 열벡터는 서포트 집합 $S$에 추가된다. 서포트 집합에 있는 열벡터들로만 구성 되어있는 행렬을 $A_{S^k}$ 로 만들면 과대 결정 행렬이 되어 최소 자승 해를 구할 수 있다. $b=A_{S^k}{x}_{S^k}$ 의 최소 자승 해를 구하여 잠정적인 해 $x^k$ 로 둔다. 이때 생기는 잔차를 새로운 잔차 벡터$r^k$ 로 갱신한다. 잔차 벡터의 l₂-norm을 초기 값 $\epsilon$과 비교하여 종료조건을 만족한다면 그 반복과정의 잠정적인 해를 최종적인 해로 도출한다. OMP는 매 반복 과정마다 잔차 벡터와 상관도가 가장 높은 열벡터를 선택함으로써 잔차 벡터의 크기를 가장 크게 감소시키는 방식으로 반복과정의 횟수, 해의 l₀-norm 을 최소화 한다.

Table 1. OMP Algorithm.

OMP 알고리즘의 종료는 초기에 입력하는 조건에 따라 두 가지 경우로 나눌 수 있다. 첫 번째의 경우는 Table 1과 같이 $\epsilon$을 초기값으로 주어 잔차의 l₂-norm과 비교하여 종료 조건으로 주는 경우이다. 두 번째 경우는 x의 l₀-norm값을 초기에 미리 설정하여 그 값만큼 반복 과정이 돌아가면 종료가 되는 경우이다. 표적의 개수를 미리 알 수 있거나 가정을 하는 경우에는 두 번째 경우의 종료 조건을 사용하고, 표적의 개수 또한 알고리즘을 통해 추정하고 자 하는 경우에는 신호 대 잡음비 값을 통해 적절한 $\epsilon$값을 도출하여 첫 번째 경우의 종료 조건을 사용한다.

3.2 CoSaMP 알고리즘

CoSaMP(Compressive Sampling Matching Pursuit) 알고리즘은 기존의 greedy 알고리즘의 단점을 보안하여 Needell과 Tropp이 새롭게 제안한 알고리즘이다.^[4] CoSaMP의 진행과정은 Table 2와 같다.

Table 2. CoSaMP Algorithm.

CoSaMP 알고리즘은 매 반복과정에서 열벡터를 선택할 때 여러 개의 열벡터를 선택한다. 초기값으로 해의 l₀-norm 값, 혹은 표적의 예상 개수를 미리 받아서 그것의 2배되는 개수만큼 열벡터를 선택한다. 해의 l₀-norm의 초기 값이 L로 주어졌다면 매 반복 과정 마다 잔차 벡터와 상관도가 높은 순서대로 2L개의 열벡터를 선택하여 서포트 집합에 추가한다. 서포트 집합의 열벡터들로 이루어진 행렬로 $b=A_{S^k}{x}_{S^k}$의 최소 자승 해를 구한다. 초기에 설정한 해의 l₀-norm에 맞게 최소 자승 해의 계수가 큰 순서대로 L개의 원소만 남기고 나머지 계수는 0으로 제거하는 작업을 완료하여 잠정적인 해를 도출한다. 잠정적인 해 인 $x^k$로부터 도출되는 잔차를 잔차 벡터로 갱신한다. 잔차벡터 의 l₂-norm이 $\epsilon$값보다 작거나 같아지면 알고리즘을 종료하고 그때의 잠정적인 해를 반환한다.

OMP 알고리즘을 포함한 기존의 greedy 알고리즘은 매 반복과정에서 잔차 벡터와 상관도가 가장 높은 열벡터를 선택했다. 이는 초기 반복과정에서의 잘못된 선택이 후의 최종적으로 잘못된 해를 도출하는데까지 직접적인 영향을 미치는 결과를 보였다. 이를 보완하기 위해 CoSaMP는 상관도가 높은 순서대로 여러 개의 열벡터를 선택하여 후에 최소 자승 해의 계수가 큰 원소들만 남기는 과정을 추가하였고, 알고리즘이 로컬 미니멈으로 빠지는 것을 방지하였다.

3.3 BPDN

압축 센싱 알고리즘의 두 번째 방식은 최적화 이론에 기반한 l₁-norm 최소화 방식이다. l₁-norm 최소화 방식 또한 충분히 희소한 해를 도출하는 것이 증명이 되어있으며^[5] 선형 프로그램으로 해를 도출할 수 있기 때문에 해석학을 이용하며 수학적으로 접근하기 쉽다. l₁-norm 최소화 방식의 Eq. (7)을 푸는 것을 압축 센싱 분야에서는 BPDN(Basis Pursuit Denoising)이라고 한다. 볼록 최적화 문제인 BPDN의 해를 도출할 수 있는 프로그램은 많이 존재한다.^[1] 그중에 본 논문에서는 BPDN을 해결하기 위해 MATLAB에서 CVX를 사용하였다. CVX 프로그램은 interior point method 알고리즘을 사용하여 BPDN문제를 해결한다.^[6]

3.4 LARS 알고리즘

Eq. (7)은 볼록 최적화 문제이므로 라그랑 승수법을 적용하여 해결할 수 있다. Eq. (7)의 제약이 없는 형식은 다음과 같다.

위 식은 통계 분야에서 회귀 분석의 한 방식으로 쓰이는 LASSO(Least Absolute Shrinkage and Selection Operator) 문제이다. 본 논문에서는 LASSO 문제를 해결하는 여러 알고리즘 중에 진행 방식이 OMP 알고리즘과 유사한 LARS(Least Angle Regression) 알고리즘을 소개한다.^[7]

Eq. (8)에서 $\lambda$는 라그랑 승수로서 l₁-norm 의 가중치 역할을 하여 해의 희소성을 결정하는 요소가 된다. $\lambda \to 0$일수록 앞항의 최소화가 가중되므로 BP(Basis Pursuit)에 가까워지며 해는 dense 해진다. $\lambda \to \infty$일수록 해는 더 희소해지는 반면에 잔차의 크기가 커진다. $\lambda$의 값에 따라 도출되는 해의 희소성이 달라지므로 적절한 $\lambda$값의 설정하는 문제가 존재한다. 이를 해결하기 위해 LARS 알고리즘은 $\lambda$값을 $\infty$에서부터 줄여가면서 희소성 값이 달라질 때의 해를 모두 구하는 방식을 사용한다. 이 방식에 greedy 알고리즘과 같이 적절한 종료조건을 주면 특정 상태에서 알고리즘이 종료되어 원하는 해를 도출할 수 있다.

종료조건을 적용한 LARS 알고리즘의 진행은 Table 3과 같다. 벡터 ${\mu }^k=A{x}^k$는 추정벡터로서 현재 잠정적인 해의 열벡터 공간에서의 위치를 나타낸다. 반복과정에서 추정 벡터가 이동할 방향과 거리를 구한다. 추정 벡터가 이동하면서 서포트 집합에 추가될 새로운 열벡터가 선택되고, 추정 벡터가 다음 위치로 이동 한 후에 반복과정이 완료된다. 추정 벡터가 이동하는 방향은 서포트 집합에 있는 열벡터들로 이루어진 행렬 $A_{S^k}$ 로부터 구한 최소 자승해$\overline{x^k}$ 가 존재하는 방향이다. $b=A_{S^k}{x}_{S^k}$ 의 최소 자승 해는$A_{S^k}$ 의 열벡터 공간에 벡터 $b$ 를 투영시킨 위치에 존재한다. 이전 반복과정에서의 추정 벡터의 위치${\mu }^{k-1}$ 에서 최소 자승 해의 위치$\overline{y^k}$ 까지의 벡터 $u^k$는 서포트 집합에 있는 열벡터들과 이루는 각이 모두 같은 등각의 방향을 갖는다. 따라서 추정 벡터가 등각의 방향으로 이동함에 따라 잔차 벡터와 서포트 집합에 있는 열벡터들과의 상관도 값은 동일하게 낮아진다. 추정 벡터가 등각 방향을 따라 이동하는 거리 $\gamma$는 서포트 집합의 열벡터들과 잔차 벡터와의 상관도와, 서포트 집합이 아닌 특정 열벡터와 잔차 벡터와의 상관도가 같아지는 최초의 지점까지의 거리이다. 상관도가 같아진 열벡터를 서포트 집합에 추가한다. 이동을 완료한 추정벡터 ${\mu }^k$로부터 잔차를 구하여 잔차 벡터를 갱신한다. 새로운 열벡터가 추가 될 때마다 잔차 벡터를 갱신하여 Eq. (7)의 $\epsilon$과 비교하여 종료 조건을 확인함으로써 최종적인 해를 도출한다.

Table 3. LARS Algorithm.

라그랑 승수법을 적용한 Eq. (8)의 해를 구하는 과정이 최소 자승 해, 등각의 벡터와 연관되는 이유는 다음과 같은 과정에서 알 수 있다. Eq. (8)의 목적함수를 $f\left(x\right)$로 나타낼 수 있다.

이 함수의 해를 구하기 위해 편미분을 한다.

볼록함수이므로 $\partial f\left(x\right)=0$이라 놓고 해를 구할 수 있다.

여기서$\lambda$는 값이 입력되었다고 가정하며, $s$는 그때의 서포트 집합을 의미한다. Eq. (11)의 괄호를 풀면 Eq. (12)와 같이 된다.

여기서 앞 항 $(A_s^T{A}_s{)}^{-1}{A}_s^{T}b$는 $A_s$의 열벡터 공간에 벡터 b를 투영시켜서 구한 최소 자승 해임을 알 수 있다. Eq. (12)의 양변에 $A_s$를 곱하여 열벡터 공간으로 옮겨 볼 수 있다.

이를 Table 3의 수식으로 표현할 수 있다.

$u_s$벡터가 등각 벡터임을 확인하기 위해 $u_s$에 $A_s^T$ 를 곱하여 보면

가 됨을 알 수 있으며 $z_{\lambda }^s=sign\left(x_{\lambda }^s\right)$ 임을 고려할 때 $u_s$는 $A_s$의 열벡터들과 상관도가 같은 벡터인 등각 벡터임을 확인할 수 있다. 이때 센싱 행렬의 열벡터의 크기는 모두 같음을 가정한다.

IV. 실 험

압축 센싱 알고리즘의 추정 성능을 비교하기 위해 두 가지 실험을 수행하였다. OMP, CoSaMP, BPDN(CVX), LARS 알고리즘에 대해 각 알고리즘이 해를 도출하는데 걸리는 시간을 측정한 계산 성능 실험과, 모의로 표적을 설정하여 각 알고리즘이 표적을 정확히 탐지하는 빈도수를 확인하는 정확도 실험을 수행하였다.

4.1 계산 성능

압축 센싱 알고리즘의 이론적인 시간 복잡도는 다음과 같다.

Table 4에서 M, N 은 센싱 행렬의 행과 열을 나타내며, K는 각 알고리즘의 반복횟수이다. CoSaMP 알고리즘의 시간복잡도는 OMP와의 비교를 위해 $O\left(MN\right)$으로 나타내기도 한다.^[9]

Table 4. Time complexity of compressed sensing algorithm.

각 알고리즘의 실제적인 계산 성능을 알기 위해 시뮬레이션을 수행하였다. 실험 환경으로 CPU Intel Core i7-6700k을 사용하였으며 MATLAB에서 실험을 수행하였다. 모의실험에 사용한 송신 신호는 Eq. (1)의 LFM신호를 사용하였다. 신호의 주기는 0.4 s, 대역폭은 300 Hz, 샘플링 주파수를 500 Hz로 설정하였으며, 도플러 bin의 개수는 5개로 주었다. 시간 지연 빈의 개수를 100개에서 50개씩 증가시켜 350개까지 변경하여 여섯 가지 경우에 대해서 실험하였다. 시간 지연 빈의 개수 조정을 통해 센싱 행렬의 크기를 변경하면서 각 알고리즘의 계산 성능을 측정하였다. 각 알고리즘의 실제적인 계산 성능을 나타낸 결과는 다음과 같다.

Table 5에서 계산 성능에 강점이 있는 greedy 알고리즘인 OMP, CoSaMP 알고리즘은 실제로 적은 시간이 걸리는 것을 확인하였다. OMP, CoSaMP, LARS 알고리즘의 시간 복잡도 표현은 같지만, 실제적인 계산 성능은 CoSaMP, OMP, LARS 순으로 좋은 결과를 보였다. l₁-norm 최소화 방식의 BPDN(CVX)는 매우 좋지 않은 결과를 보였지만 greedy한 특성이 추가된 LARS 알고리즘은 greedy 알고리즘의 계산 성능에 가까운 결과를 보였다.

Table 5. Computational performance measurement results of compressed sensing algorithms(s).

4.2 정확도

본 논문에서는 상호 간섭성과 신호 대 잡음 비 가 각 알고리즘의 정확도에 미치는 영향을 확인하였다. 특정 상호 간섭성 값을 갖도록 센싱 행렬을 생성한 후에, 신호 대 잡음비 값을 변경하면서 해를 도출하여 표적 탐지의 정확도를 계산하였다. Eq. (3)에서 샘플링 주파수를 변경함으로써 센싱 행렬의 상호 간섭성 값을 변경하였으며, 상호 간섭성 값이 0.05 ~ 0.8 사이를 갖도록 하였다. 표적은 바로 인접한 위치에 두어, 두 표적의 신호의 상관도가 센싱 행렬의 상호 간섭성과 같은 값을 갖도록 하였다. 상호 간섭성 이외의 변인 통제를 위해 도플러 효과는 주지 않고 시간 지연만 주어 센싱 행렬을 생성하였다.

각 알고리즘의 정확도는 오차율을 측정하여 나타냈다. 알고리즘에 의해 도출된 해가 정확히 두 표적의 거리를 나타내는 인덱스에서만 임계값을 넘는 값을 나타낼 경우를 성공으로 두었으며 성공이 아닌 경우는 모두 오차로 두었다. 두 표적 신호에 특정 신호 대 잡음 비 값에 해당하는 소음을 줄 때 백색 가우시안 소음을 주어 랜덤하게 수신 신호 $b$를 생성하였으며, 몬테 카를로 방법을 통해 1000번의 반복 실험을 하여 표본 공간을 생성하였다. 모의실험에 사용한 송신 신호는 Eq. (1)의 LFM신호이다. 신호의 주기는 0.4 s, 대역폭은 300 Hz, 시간 지연 bin은 200개로 주었다. 샘플링 주파수는 300 Hz에서 900 Hz까지 변경해가며 실험하였다. Eqs. (3)과 (4)에 의해 샘플링 주파수를 높일수록 센싱 행렬의 상호 간섭성 값이 증가하며, 한 개의 시간 지연 빈 차이가 나타내는 거리는 감소함을 알 수 있다. 음파의 수중 속도를 고려하여 계산한 인접한 두 표적의 거리는 상호 간섭성 값이 0.05, 0.8일 때 각각 2.5 m, 0.9 m이다.

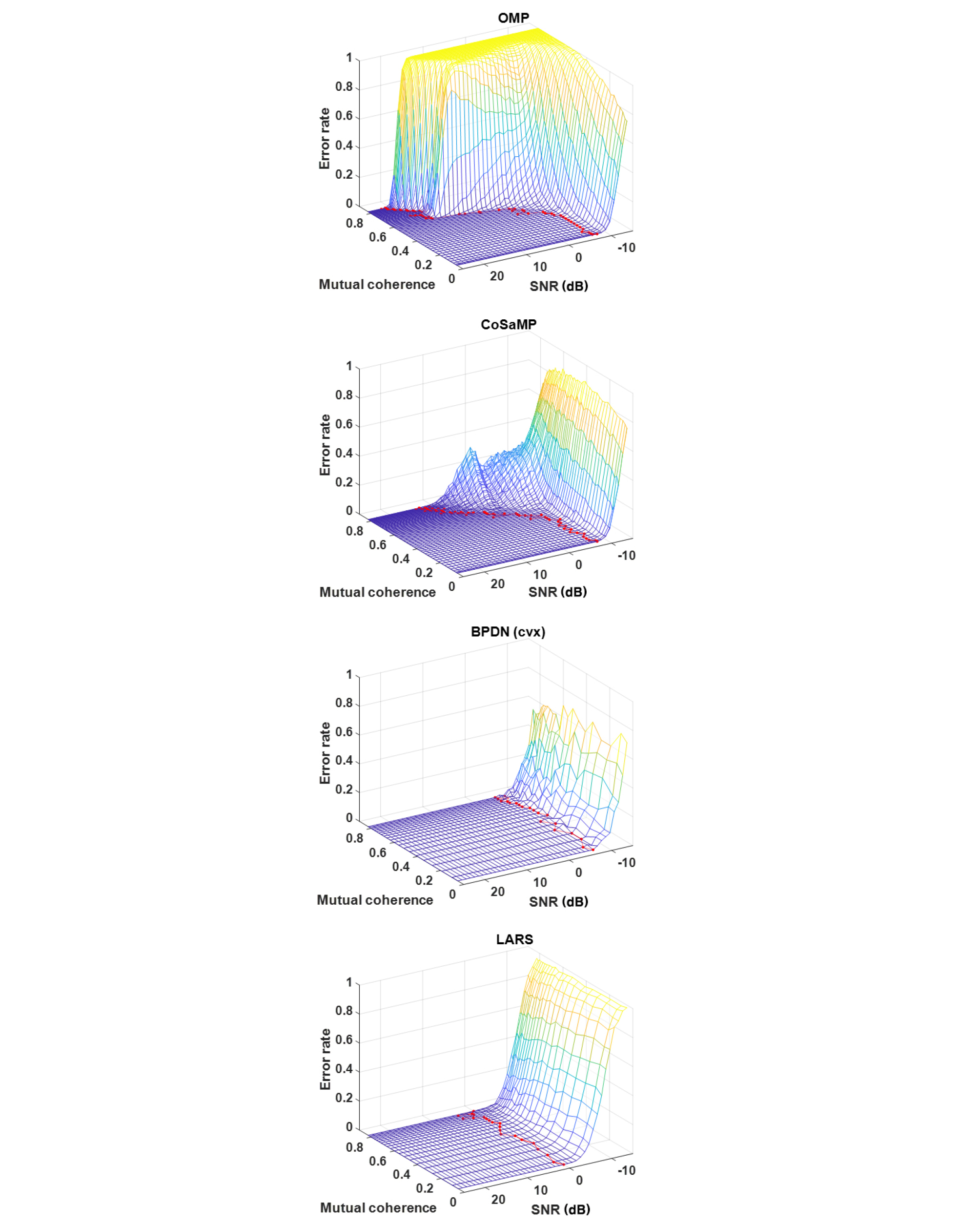
Fig. 1은 OMP, CoSaMP, BPDN(CVX), LARS 알고리즘에 대한 시뮬레이션 결과를 보여준다. OMP, CoSaMP 알고리즘이 해당되는 l₀-norm 최소화 방식의 정확도는 상호 간섭성, 혹은 두 표적 신호의 상관도에 큰 영향을 받는 반면에 BPDN(CVX), LARS 알고리즘이 해당되는 l₁-norm 최소화 방식의 정확도는 상호 간섭성 에 크게 영향 받지 않는 것을 확인하였다. 상호 간섭성 값이 0.5를 넘어가면서 OMP, CoSaMP 알고리즘의 성능이 급격하게 저하되는데, 이는 두 표적의 위치가 1.5 m보다 가까워지는 기점이다. 기존의 greedy 알고리즘을 개선한 CoSaMP 알고리즘은 OMP 알고리즘 보다 전반적으로 정확도 측면에서 좋은 성능을 보임을 확인하였으며, l₁-norm 최소화 방식에 greedy 한 특성을 적용한 LARS알고리즘은 BPDN(CVX) 보다 좋지 않은 성능을 보임을 확인하였다.

Fig. 1.

3D curve of error rate regarding range-dop-pler resolution (coherence), SNR (Signal to Noise Ratio) dotted line represents the minimum SNR with an error of zero for every simulated mutual coherence.

V. 결 론

압축 센싱 알고리즘에 따라 계산 성능과 정확도가 다름을 확인하였다. 센싱 행렬의 코히런스가 높지 않은 상황에서는 greedy 알고리즘 기반의 l₀-norm 최소화 방식 알고리즘이 시간 측면에서 유리하고, 센싱 행렬의 코히런스가 높은 상황이라면 최적화 이론 기반의 l₁-norm 최소화 방식 알고리즘을 사용하는 것이 정확도 측면에서 손실이 없다. 추가적으로 엄밀한 정확도가 요구되는 상황이라면 BPDN(CVX)를 사용하고, 그렇지 않은 전반적인 상황에는 LARS 알고리즘이 시간 측면과 정확도 측면에서 적합하다.