I. 서 론

적응 필터는 신호처리 분야의 한 종류로서, 음성 신호처리 분야나 수중 음향 채널 추정 및 등화기 설계에 많이 쓰인다.^[1],[2],[3] 특히 채널 추정에서 신호처리 대상이 되는 채널의 상당수는 희소성을 갖는다고 알려져 있다. 이는 임펄스 응답이 길지만 소수의 탭만이 ‘0’이 아닌 특징을 지니는 채널을 의미한다. 이런 특징을 갖는 채널은 수중 음향 채널 및 여러 통신 채널 등에서 자주 접할 수 있다.^[4],[5] 그러나 Least Mean Squares(LMS)나 Recursive Least Squares(RLS)같은 전통적인 오차의 최소 자승을 목적함수로 하는 적응 신호처리 알고리즘들은 이 같은 희소성 채널에서 충분한 우수성을 나타내지 못하고 있다.

지난 십여 년간 희소성을 직접 이용하는 알고리즘을 개발하는 활발한 노력이 있어 왔다.^[6],[7],[8] 이런 연구 결과의 예로 LMS 분야에서는 l₀-norm을 적용한 l₀-LMS가 있고,^[9]l₁-norm을 적용한 l₁-LMS가 있다.^[10] RLS 분야에서도 l₁-norm을 적용한 사례 중 대표적인 것을 Eksioglu와 Tanc가 Reference [11]에서 l₁-norm RLS로 제안하였다. 이 알고리즘은 완벽하게 RLS를 기반 한 방법으로써 그 후 여러 연구자들에 의해 참고 되어 오고 있다. 그러나 RLS를 사용하는 알고리즘들은 일반적으로 입력 신호 자기상관 행렬의 역행렬 계산에서 불안정해지는 경향이 있다. 이런 수치상 불안정 상태의 주된 원인중 하나가 ${\mathbf{R}}_{\mathbf{xx}}\left(n\right)={\mathbf{R}}_{\mathbf{xx}}(n-1)+\mathbf{x}\left(n\right)\mathbf{x}(n{)}^T$로 계산되는 자기상관 행렬의 역행렬에 대칭성이 유지되지 못할 때라는 것이 알려져 있고, 이런 수치적 불안정은 상관 행렬 ${\mathbf{R}}_{\mathbf{xx}}\left(n\right)$을 추정할 때 대칭이 깨지기 때문이라는 것임도 알려져 있다.^[1] 따라서 Reference [11]의 l₁-norm RLS 역시 같은 수치적 불안정성을 지니고 있다.

본 논문은 Reference [11]에서 제안된 l₁-norm 규준화를 사용한 RLS방법에 Reference [12]에 제안된 최소자승 백색화 기법을 적용하여 희소성에 잘 대응하면서, 수치계산에서 오는 불안정성에 견실함도 더한 알고리즘을 제안한다. 이를 위해서 본 논문은 II장에 Reference [11]에서 제안한 볼록 규준화를 사용한 RLS방법을 정리하고, III장에서는 Reference [12]에서 제안한 백색화를 적용하기 위한 수식적인 변형을 알아보고 이 백색화를 적용한 볼록 규준화 RLS방법을 제안한다. IV장에는 다양한 양자화 단계로 신호를 양자화 함으로써 수치적 불안정성을 생기게 하고 이에 대해서 새로 제안한 알고리즘과 기존의 알고리즘간의 성능을 Mean Square Deviation(MSD)를 척도로 사용하여 서로 비교한다.

II.볼록 규준화를 사용한 RLS방법^[1]

추정 대상이 되는 희소채널의 입력과 출력 간의 관계를 다음 식으로 나타낸다.

여기서 $y\left(n\right)$는 출력 신호이고, $\mathbf{x}\left(n\right)={\left[x\left(n\right),\cdots ,x(n-L+1)\right]}^T$는 L차 입력 신호 벡터이다. ${\mathbf{w}}_o$는 희소성 채널의 참 임펄스 응답이고, $\eta \left(n\right)$는 부가 잡음이다. RLS를 위한 목적함수는 다음과 같은 망각인자를 사용한 오차 에너지 식을 사용한다.

여기서

$e\left(n\right)=y\left(n\right)-\hat{\mathbf{w}}\left(n{)}^T\mathbf{x}\right(n)=[{{\mathbf{w}}_{\mathit{o}}}^{\mathbf{T}}-\hat{\mathbf{w}}\left(n{)}^T\right]\mathbf{x}\left(n\right)+\eta \left(n\right).$

위 목적함수에 희소성 채널을 추정하기 위해서 다음 식과 같이 규준화 항을 추가한다.

여기서 $\gamma \left(n\right)$는 $l_1$형식 규준화 상수이고 $f\left(\hat{\mathbf{w}}\right)=||\hat{\mathbf{w}}||{}_1=\sum _{k=0}^{L-1}\left|{\hat{w}}_k\right|$이다. 위 목적함수를 최소화하기 위해서 다음과 같이 양변에 미분을 취하여 그를 ‘0’로 하는 항을 구한다.

여기서 ${\nabla }^s$는 위 규준화 함수와 같은 일반적으로 미분되지 않은 함수에 정의한 확장된 미분자(subgradient operator)를 의미한다. 위의 $l_1$형식 규준화를 위한 확장 미분자는 ${\nabla }^s\left({||\hat{\mathbf{w}}||}_1\right)=\mathrm{sign}\left(\hat{\mathbf{w}}\right)$이다. 여기서 sign ( )은 양수이면 ‘1’이고, 음수이면 ‘0’을 내는 함수이다. 위와 같은 미분을 통해서 다음과 같은 정규 방정식을 구할 수 있다.

여기서

$\mathit{\Phi }\left(n\right)=\sum _{m=0}^n{\lambda }^{n-m}x\left(m\right)x(m{)}^T=\lambda \mathit{\Phi }(n-1)+\mathbf{x}(n\left)\mathbf{x}\right(n{)}^T$

이고

$\mathbf{r}\left(n\right)=\sum _{m=0}^n{\lambda }^{n-m}y\left(m\right)\mathrm{x}\left(m\right)=\lambda \mathbf{r}(n-1)+y\left(n\right)\mathbf{x}\left(n\right)$이다. 그리고 위 식으로부터 새 변수 $\theta$을 아래와 같이 새로 정의한다.

Eq. (6)으로부터 다음과 같은 제차형 갱신식을 구한다.

Eq. (7) 양변에 $\mathbf{P}\left(n\right)=\mathit{\Phi }(n{)}^{-1}$를 곱하고 $\hat{\mathbf{w}}\left(n\right)=\mathbf{P}\left(n\right)\mathit{\theta }\left(n\right)$를 사용하면 다음과 같다.

여기서 $\mathbf{P}\left(n\right)=\frac{1}{\lambda }\left[\mathbf{P}\right(n-1)-\mathbf{k}(n\left)\mathbf{x}\right(n{)}^T\mathbf{P}(n-1)]$, $\mathbf{k}\left(n\right)=\mathbf{P}\left(n\right)\mathbf{x}\left(n\right)$이고 $ϵ\left(n\right)=y\left(n\right)-\hat{\mathbf{w}}(n-1{)}^T\mathbf{x}(n)$이다. 위 식은 Eksioglu와 Tanc가 Reference [11]에서 제안한 볼록 규준화를 사용한 RLS방법이다. Reference [11]에서는 위 식에서 규준화 상수를 다음과 같이 유도 하였다.

여기서 $\mathit{\epsilon }\left(n\right)=\hat{\mathbf{w}}\left(n\right)-{\hat{\mathbf{w}}}_{RLS}\left(n\right)$이고 ${\hat{\mathbf{w}}}_{RLS}\left(n\right)$는 전통적인 RLS로 얻는 추정 채널 벡터이다. 또 $\rho$ 상수는 여러 연구를 통해서 상수 값을 정하는 법이 발표되어 있지만 본 논문의 취지와 직접적으로 맞지 않아서, 본 논문에서는 가장 이상적인 경우인 채널의 참 임펄스 응답으로부터 $\rho =$‖채널파라메터 벡터의 참값‖₁, 즉 $\rho ={||w_o||}_1$ 같이 설정하여 사용한다.^[11]

III. 백색화 (prewhitening)를 적용한 볼록 규준화된 RLS

본 절에서는 Douglas가 제안한 최소자승 백색화 기법을 앞 절에서 정리한 볼록 규준화된 RLS 알고리즘에 적용한다.

$\mathbf{P}\left(n\right)=\mathit{\Phi }(n{)}^{-1}$을 $(L\times L)$크기의 임의의 행렬의 곱으로 Q^T(n)Q(n)로 대치하면 (단 그 의미는 다음 단락에서 설명),

$\mathit{k}\left(n\right)=\frac{\mathbf{P}(n-1)\mathbf{x}\left(n\right)}{\lambda +{\mathbf{x}}^T\left(n\right)\mathbf{P}(n-1)\mathbf{x}\left(n\right)}$가

로 된다. 또 $\mathbf{P}\left(n\right)=\frac{1}{\lambda }\left[\mathbf{P}\right(n-1)-\mathbf{k}(n\left)\mathbf{x}\right(n{)}^T\mathbf{P}(n-1)]$는

로 변환된다. 여기서 $\mathbf{v}\left(n\right)=\mathbf{Q}(n-1)\mathbf{x}\left(n\right)$이다. 이 때 벡터 v(n)는 다음 특성을 가진다.^[12] 즉, 만약 y(n)가 Wide Sense Satationary(WSS)이라면,

이는 Q(n)가 수렴함에 따라, v(n)의 요소들은 서로 상관성이 없고 또 각 파워는 (1-λ)에 수렴한다는 뜻으로 해석할 수 있다.^[12] 또 이 성질은 일종의 백색화 과정이라고 생각할 수 있다. Eq. (11)의 오른쪽 변의 대괄호 부분은 다음과 같이 행렬 곱으로 분해할 수 있다.

Eq. (13)를 이용하면 Eq. (11)에서 Q(n)은 다음과 같이 갱신될 수 있음을 알 수 있다.

Eq. (13)의 오른쪽 변은 다음과 같이 변형할 수 있다.

Eq. (15)에서 $\frac{\mathbf{v}\left(n\right){\mathbf{v}}^T\left(n\right)}{\parallel \mathbf{v}\left(n\right){\parallel }^2}=\mathbf{v}\left(n\right){\left({\mathbf{v}}^{\mathbf{T}}\left(n\right)\mathbf{v}\left(\mathrm{n}\right)\right)}^{-1}{\mathbf{v}}^{\mathrm{T}}\left(\mathrm{n}\right)$는 $\mathbf{v}\left(\mathrm{n}\right)$ 공간으로의 투영을 의미한다. 즉 신호 공간에로의 투영을 의미한다. 반면에 $\mathbf{I}-\frac{\mathbf{v}\left(n\right){\mathbf{v}}^T\left(n\right)}{\parallel \mathbf{v}\left(n\right){\parallel }^2}$는 신호공간과 직교인 잡음공간으로의 투영을 의미한다. 또 부가로 ${\mathbf{B}}^T\left(n\right)\mathbf{B}\left(n\right)$는 $\frac{\lambda }{\lambda +\parallel \mathbf{v}\left(n\right){\parallel }^2}$의 고유치 하나를 가지고, 나머지 차원은 잡음공간으로 1의 고유치를 가짐을 알려주고 있다. $\mathbf{I}-\frac{\mathbf{v}\left(n\right){\mathbf{v}}^{\mathbf{T}}\left(n\right)}{\parallel \mathbf{v}\left(n\right){\parallel }^2}$과 $\frac{\mathbf{v}\left(n\right){\mathbf{v}}^{\mathbf{T}}\left(n\right)}{\parallel \mathbf{v}\left(n\right){\parallel }^2}$의 대칭성과 직교성을 이용하면, B^T(n)B(n)의 대칭 평방근 인자는

이 됨을 알 수 있다. Eq. (14)에 Eq. (16)을 대입하여 다음과 같은 갱신식을 얻게 된다.

Eq. (8)에 Eq. (14) 및 Eqs. (17) ~ (20)을 적용하면, 새로운 백색화 볼록 규준화 RLS알고리듬을 얻게 된다. 알고리듬의 복잡함은 기존의 RLS알고리듬과 유사하나 알고리듬의 견실성은 월등히 향상된다.

백색화를 적용하여 볼록 규준화를 사용한 RLS방법를 다시 쓰면 Table 1과 같이 정리된다.

Table 1. Prewhitened l₁-regularized RLS.

IV. 시뮬레이션

시뮬레이션을 위해서 참 채널 임펄스 응답의 길이는 L = 64로 정하였다. 그리고 매 번의 반복 실험 때 마다 총 64개 탭 중에서 2개의 탭을 불규칙하게 뽑아서 희소성 채널을 구성하도록 하였다. 또 백색화의 효과를 보이기 위해서 유한 비트로 신호를 양자화 하여 연산하는 경우를 설정하였다. 양자화를 할 때 Table 1의 각 단계마다 양자화를 실시하였고, 입력 신호도 양자화를 적용하였습니다.

유한 비트로 양자화 하는 설정을 한 이유는 양자화 잡음 상황을 유도하여 알고리즘 연산중에 수치적 오류를 유도하고 이를 통해서 ${\mathbf{R}}_{\mathbf{xx}}\left(n\right)$의 역행렬 연산에 오류가 포함되도록 만들기 위해서이다. 이런 상황을 보이기 위해서 양자화 비트 수를 12비트, 16비트 및 32비트로 바꿔서 성능을 비교 검증하도록 하였다. 채널에 입력으로 사용하는 신호는 평균은 0, 분산은 1인 정규분포를 갖는 불규칙 수를 발생하여 사용하였다. 그리고 출력신호에 부가되는 잡음 수준은 출력의 신호 대 잡음비를 20 dB가 되도록 부가하였다.

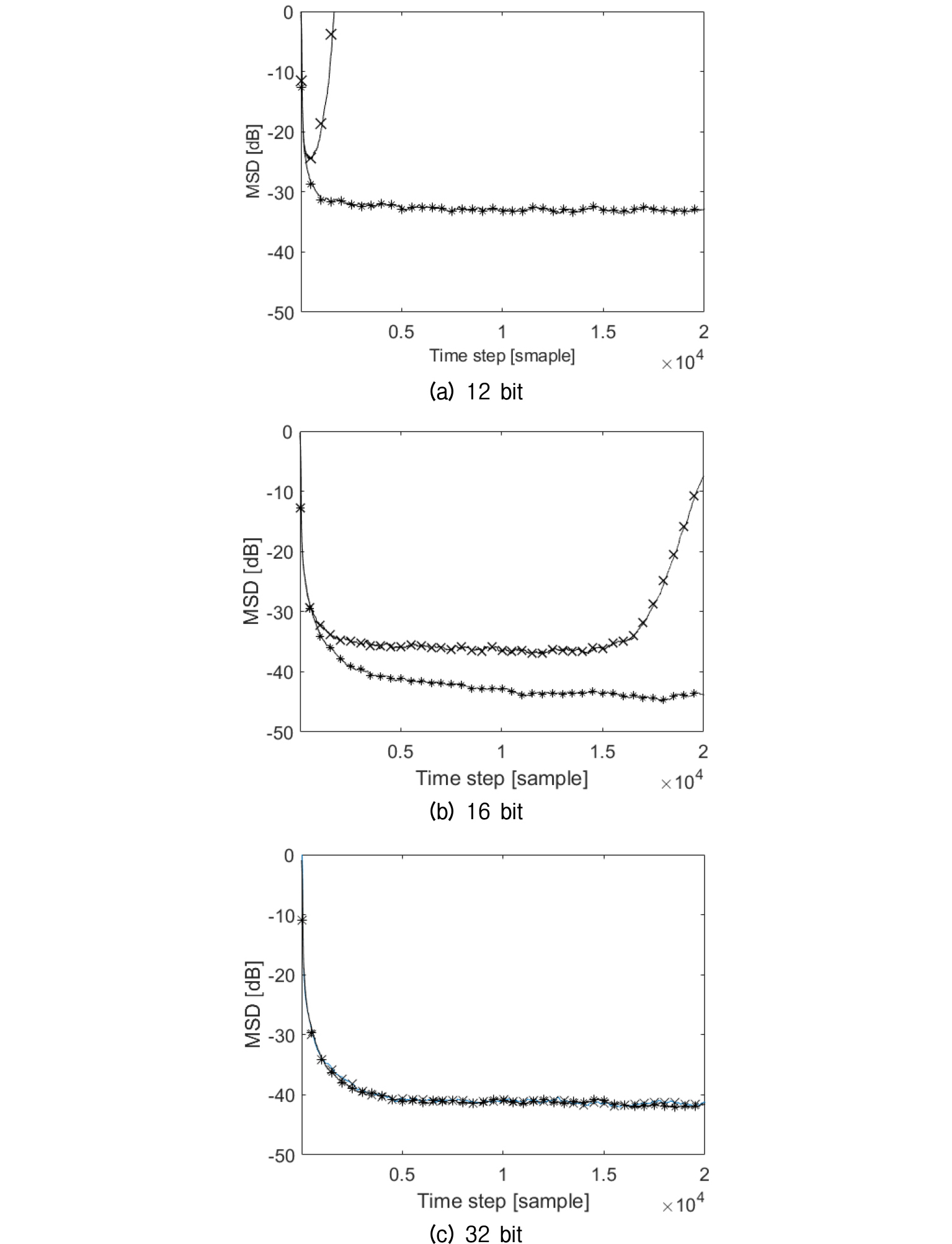
Fig. 1은 각각 다른 양자화 비트 수에 상황에서 제안된 알고리즘과 기존 알고리즘을 각각 MSD 측면에서 서로의 성능을 비교한 결과를 보였다, 여기서 $\mathrm{MSD}=E\left(|\hat{\mathbf{w}}-{\mathbf{w}}_{\mathrm{true}}{|}^2\right)$.

Fig. 1.

Comparison between conventional l₁-RLS and the proposed algorithm (-x-: the conventional l₁-RLS , -*-: the proposed algorithm).

Fig. 1(a)는 12 bit로 양자화된 경우의 결과이다. 일반적인 알고리즘은 양자화 잡음의 오차의 누적전달 효과에 의해서 일찍부터 발산하는 것을 관찰 할 수 있다. 반면에 백색화를 적용한 제안된 알고리즘은 정상적으로 수렴이 됨을 관찰 할 수 있다. Fig. 1(b)는 16 bit로 양자화된 경우의 결과이다. 일반적인 알고리즘은 12 bit일 때 보다 약간 더디긴 하지만 양자화 잡음의 오차의 누적전달 효과에 의해서 발산하는 것을 관찰 할 수 있다. 반면에 백색화를 적용한 제안된 알고리즘은 정상적으로 수렴이 됨을 관찰 할 수 있다. 마지막으로 Fig. 1(c)는 32 bit로 양자화된 경우의 결과이다. 이 경우는 백색화를 적용한 제안된 알고리즘뿐만 아니라 일반적인 알고리즘 또한 정상적으로 수렴이 됨을 관찰 할 수 있다.

V. 결 론

본 논문에서는 Eksioglu와 Tanc가 Reference [11]에서 제안한 l₁놈을 사용한 RLS방법에서 수치적인 안정성을 더한 새 방법을 제안하였다. 그리고 이를 여러 가지 양자화 잡음이 있는 상황에서 희소성 채널을 추정해보고, 그 결과가 Reference [11]에서 제안된 방법에 비하여 더 안정함을 보였다.